R的简单教程--03进阶-2

r-rbase

华中科技大学–组学数据分析与可视化课程–大二上课程笔记第三部分，包括并行计算、ggplot2基础、常用统计学函数、参数/非参数检验、线性/非线性回归等

写在前面：本篇内容及例子（除标注了参考文章/具体案例的部分，以及一些比较零碎的小知识点）均来自华中科技大学–组学数据分析与可视化课程–大二上 / 笔记中使用的数据 / 关于本课程的复习资料 / 课程作业答案 / 课程作业答案–中文注释版

并行计算

即同时执行多个计算任务以加速整体的处理速度，通过在多个处理器或多个计算节点上同时执行代码来实现

一般需要3个步骤：

分解并发放任务
分别计算
回收结果并保存

相关的包：

parallel包：显示CPU core数量，将全部或部分CPU核心分配给任务。在任务完成后，要回收分配的CPU core
foreach包：提供%do%和%dopar%操作符，以提交任务，进行顺序或并行计算
辅助包iterators：将data.frame、tibble、matrix等数据结构分割为行/列，用于提交并行任务

install.packages( "parallel" );
install.packages( "foreach" );  # 会自动安装 iterators 

一个简单的例子：

library(parallel); 
library(foreach);
library(iterators);
# 检测有多少个CPU core
cpus <- parallel::detectCores();  # 返回一个整数，表示CPU core数量
# 创建一个data.frame 
d <- data.frame(x=1:10, y=rnorm(10));
# 创造一个cluster集群进行计算
cl <- makeCluster( cpus - 1 );
# 分配任务
res <- foreach( row = iter( d, by = "row" ) ) %dopar% {
  return ( row$x * row$y  );
}
# 注意在最后关闭创建的cluster，释放资源
stopCluster( cl );

补充说明：

res <- foreach( row = iter( d, by = "row" ) ) %dopar% {
  return ( row$x * row$y  );
}

其中：

row = iter( d, by = "row" )表示将输入数据d按行row或列col遍历，每次取出一行/一列，赋予row这个变量（可随意取名）
foreach函数将数据row分发给cl（这里没有体现出来），进行计算row$x * row$y，并返回结果
.combine = 'c'参数规定将返回结果合并为vector

该参数的可能值：
- 'c'将返回值合并为vector，当返回值是单个数字或字符串的时候使用
- 'cbind'将返回值按列合并
- 'rbind'将返回值按行合并
- 默认情况下返回list

foreach函数的其它参数.packages=NULL：将需要的包传递给任务，例如当每个任务需要提前装入tidyverse包时，可以.packages=c("tidyverse")

嵌套foreach：有些情况下需要用到嵌套循环，使用以下语法–

foreach( ... ) %:% {
  foreach( ... ) %dopar% {
    # 语句
  }
}

即外层的循环部分用%:%操作符

例：将下面的计算转为并行计算

mtcars %>% 
    split( .$cyl ) %>% 
    map( ~ cor.test( .$wt, .$mpg ) ) %>% 
    map_dbl( ~.$estimate );

运行结果为：

         4          6          8 
-0.7131848 -0.6815498 -0.6503580 

使用并行计算：

cpus <- parallel::detectCores();
cl2 <- makeCluster( cpus - 1 );
res2 <- foreach( 
    df = iter(  mtcars %>% split( .$cyl )  ), 
    .combine = 'rbind' 
    ) %dopar% {
        cor.res <- cor.test( df$wt, df$mpg );
        return ( c(cor.res$estimate, cor.res$p.value) );  #注意这里的返回值是vector
    }
res2;

df = iter(mtcars %>% split( .$cyl ))：将mtcars按汽缸数cyl分割为3个list，依次赋予df
cor.res <- cor.test(df$wt, df$mpg);：计算每个df中wt与mpg的关联，将结果保存在cor.res变量中
.combine = 'rbind'：由于返回值是vector，用此命令按行合并

运行结果为：

                cor           
result.1 -0.7131848 0.01374278
result.2 -0.6815498 0.09175766
result.3 -0.6503580 0.01179281

其中第二列是p值，第一列就是上面普通计算得到的结果

其它并行计算函数：parallel包本身也提供了lapply等函数的并行计算版本，包括parLapply、parSapply、parRapply、parCapply等

例：计算2的N次方

cl<-makeCluster(3);
parLapply(
  cl,  # 使用cl集群计算
  2:4,  # 要遍历的数据
  function(exponent)  # 将每个元素传给exponent
    2^exponent  # 返回2的exponent次方
);
stopCluster(cl);

运行结果为一个列表：

[[1]]
[1] 4

[[2]]
[1] 8

[[3]]
[1] 16

ggplot2基础

一篇很好的ggplot2基础教程

基本参数

ggplot(data, aes(x, y, colour, fill, shape, size, group,...)) +
  geom_<layer_name>() +
  其它控制函数

data标识使用的数据集
aes(aesthetics)美学：控制全局参数，包括x,y轴使用的数据、颜色(colour、fill) 、形状 (shape)、大小(size)、分组(group)等等
geom_<layer_name>绘制不同的图层：每张图可有多个图层，每个图层都可使用全局数据(data)和参数(aes)，也可以使用自己函数中指定的aes和数据
ggplot()主函数与其它函数间使用+连接

一个例子：

准备数据

year1 <- c(7, 12, 28, 3, 41);
year2 <- c(14, 7, 6, 19, 3);
df <- rbind( 
  tibble( month = 1:length( year1 ), value = year1, cat = "Year1" ),
  tibble( month = 1:length( year2 ), value = year2, cat = "Year2 ") 
);

ggplot基本参数1

画图，并将结果保存都变量中

plot1 <-  ## 将图保存在变量中；
  ggplot( df, aes( x = month, y = value, colour = cat) ) +  # 指定数据、xy轴使用哪列、根据哪列区分不同颜色
  geom_line() +  # 画折线
  geom_point() +  # 画点
  xlab( "Month" ) + ylab( "Rain fall" ) +  # 指定xy轴名称
  labs( colour = "Year");  # 图例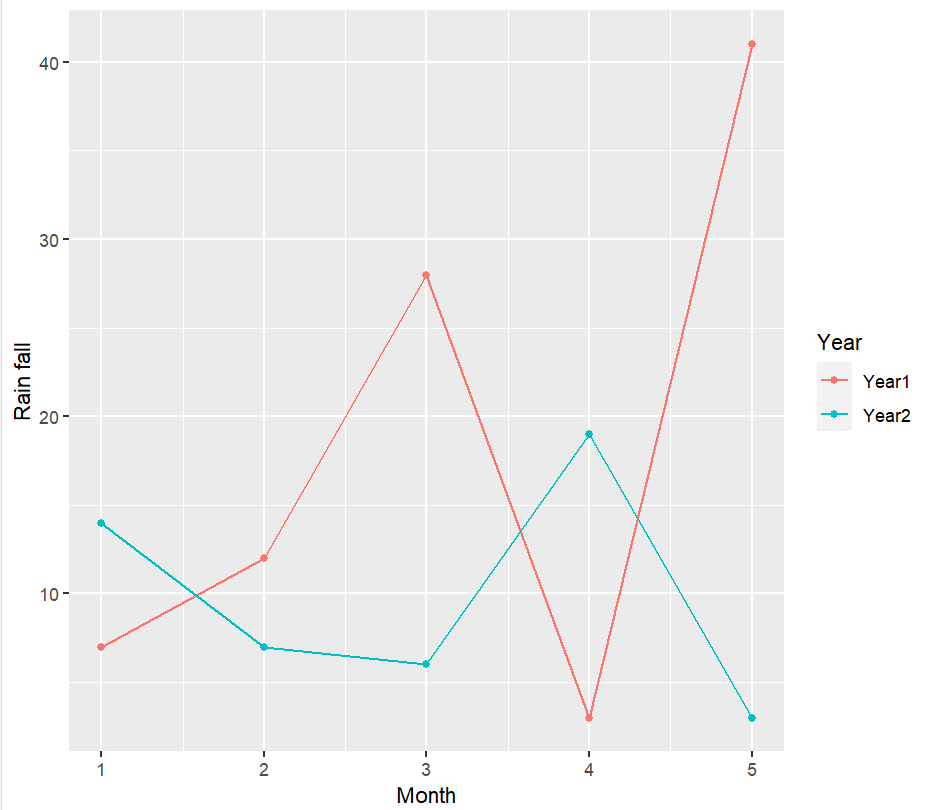

ggplot基本参数2

添加新图层，新图层使用自己的数据

plot1 + 
  geom_point( 
    data = data.frame( x2 = 1:5, y2 = sample(30:100, 5) ),  # 注意data=是必须的
    aes( x = x2, y = y2 ),  # 使用自己的aes
    colour =  c("darkgreen", "red", "blue", "gold", "purple") , 
    shape = 15, 
    size = 4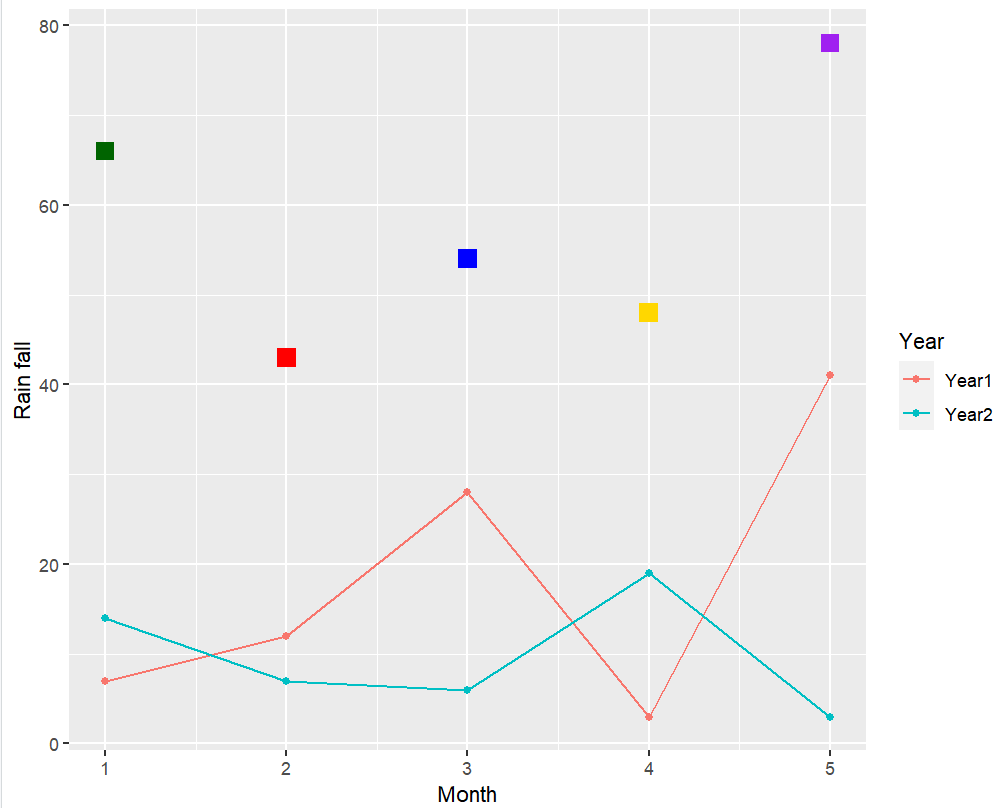 
  );

ggplot基本参数3

从上面的例子中可以发现：

xy轴范围会随数据自动调整
ggplot2作图结果可以保存在变量中，并可在其基础上累加更多图层
图层使用自己的数据时，需要用data=指定；而全局数据（ggplot(data,aes())）则不用

ggplot2作图的四个基本组成部分

图层：geom_<图层名>
- geom_point/geom_line：点/线图，用于揭示两组数据间的关系
- geom_smooth：拟合曲线图，常与geom_point联合使用，揭示数据走势
- geom_bar：条形图
- geom_boxplot：箱线图，用于比较N组数据，揭示区别
- geom_path：与geom_line相似，但也可以画其它复杂图形
- geom_histogram/geom_density：数据的分布，也可用于多组数据间的比较
scale显示控制，基本语法为scale_<控制内容>_<控制手段>，例如scale_color_manual表示以手选方式(manual)控制颜色(color)

4种基本控制：
- scale_color_...（边框）颜色
- scale_fill_...填充颜色（如果图中的点支持填充的话，如果不支持就只有color）
- scale_shape_...形状
- scale_size_...尺寸
坐标系统coord_...
- 线性坐标系统：
  - coord_cartesian默认使用的坐标系统，可以实现局部缩放的效果
  - coord_flip交换xy轴
  - coord_fixed用特定的长宽比例作图
- 非线性坐标系统：
  - coord_trans对x/y轴进行变换，如让y轴取原来的log10，这样就得到不均匀的y轴
  - coord_polar极坐标图，可以实现柱图变饼图
  - coord_map用于地图的绘制
子图facet_...：将一个数据集用多个子图来表示，每个子图表示数据集的不同子集
- facet_grid指定将数据集按哪列分组进行子图的绘制
- facet_wrap指定子图的排列（几行几列、方向等）

之后会从这4部分完成对ggplot2基础的介绍

scale显示控制

color

一个关于颜色的简单图：

ggplot(iris,  # 使用iris数据
       aes(
         x=Sepal.Length,  # 长度
         y=Sepal.Width,  # 宽度
         color=Species  # 同物种的数据点有相同颜色
         )) +
  geom_point(size=2);  # 画散点图

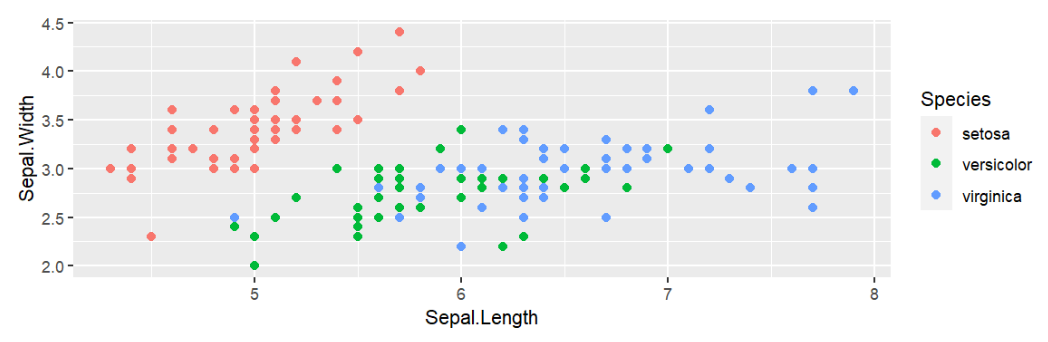
color1

可以看到：

color=Species指定了根据Species列决定颜色
共需要3种颜色
此时的颜色由默认色板决定

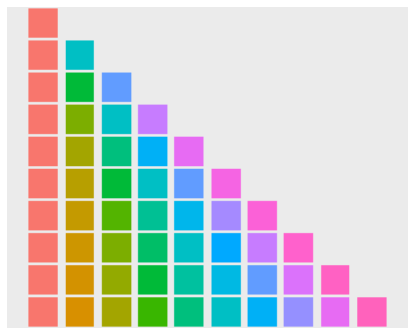
根据需要的颜色数量，取相应的行

使用其它色板：scale_colour_brewer(palette="<palette name>")

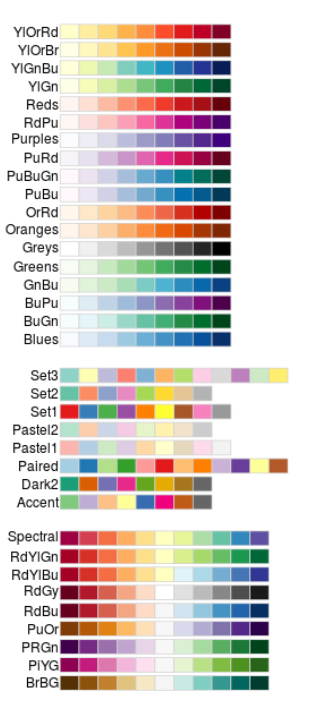
color3

左侧为色板名称，右侧为其包含的颜色。使用时需要几种颜色，就取其前几种颜色

例：

ggplot(iris, aes(x=Sepal.Length, y=Sepal.Width, color=Species)) +
  geom_point(size=2) + 
  scale_color_brewer( palette = "Set1" );

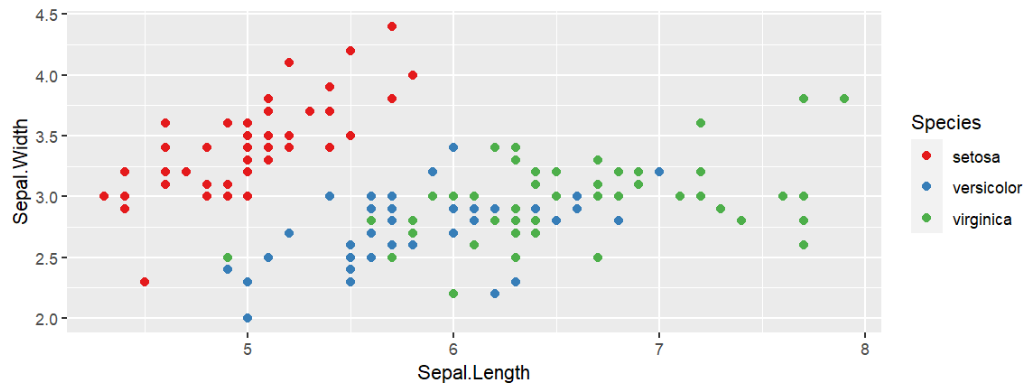
color4

手动设置颜色：scale_colour_manual(break=c(值1, 值2, ...), values=(c(颜色1, 颜色2, ...)))

在此之前，需指定颜色根据哪列来取，该列值为值1的点颜色为颜色1

mtcars %>% 
  ggplot( aes(disp, mpg) ) + 
    geom_point( aes( color = factor(cyl) ) ) +
  # 也可以写成
  # ggplot(aes(x=disp, y=mpg, color=factor(cyl))) +
  #   geom_point() +
    scale_color_manual( 
      breaks = c("4","6","8"),  # cyl列值为4的点颜色为红色...
      values = c("red","green","blue") 
    );

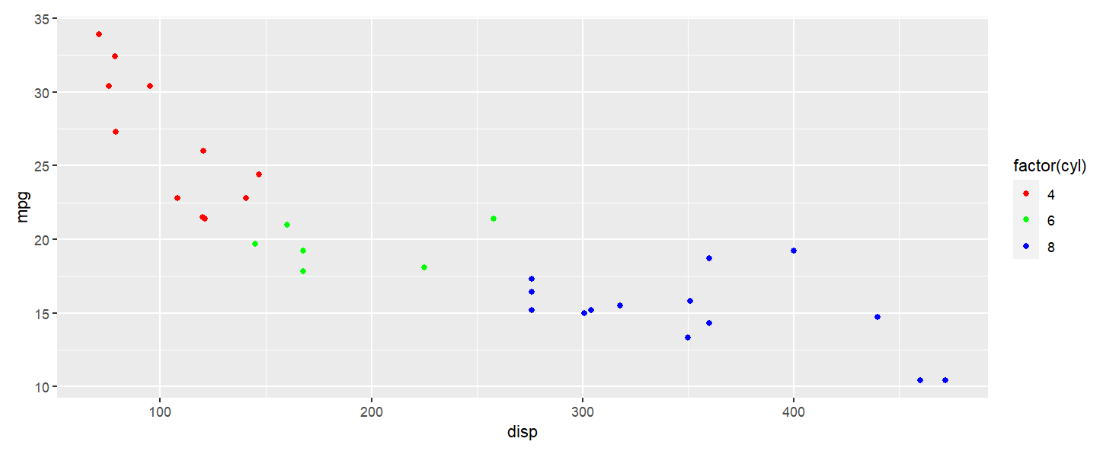
color5

注意：使用该方法指定颜色根据哪列来取时，不能使用color=列名的方法，必须为color=factor(列名)，这是因为这个方法只能用于列值为离散值的情况，factor函数用于将这列的列值去重提取，便于与scale_colour_manual函数中的breaks参数适配

使用渐变颜色：scale_color_gradient(low=颜色1, high=颜色2)即为颜色1->颜色2的渐变

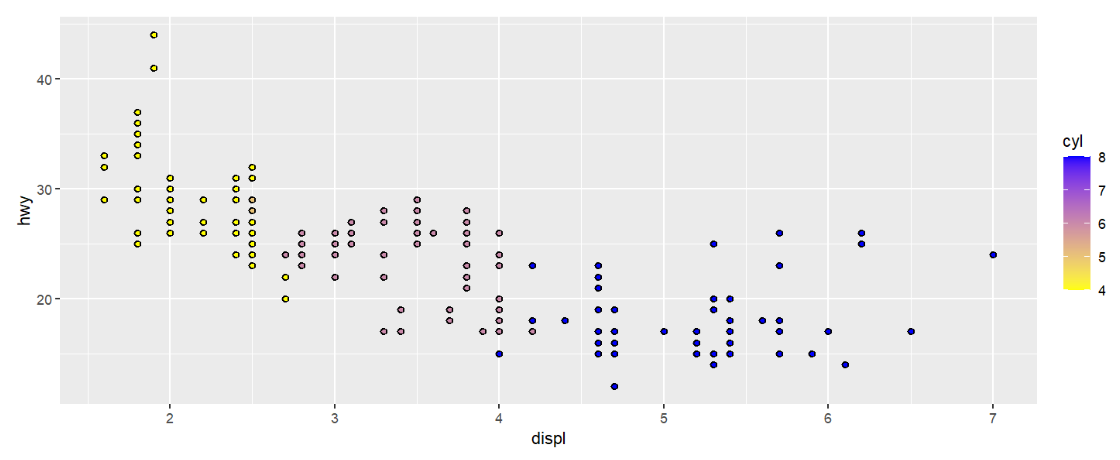
mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( color = displ ) ) +
  scale_color_gradient( low = "black", high = "yellow" );

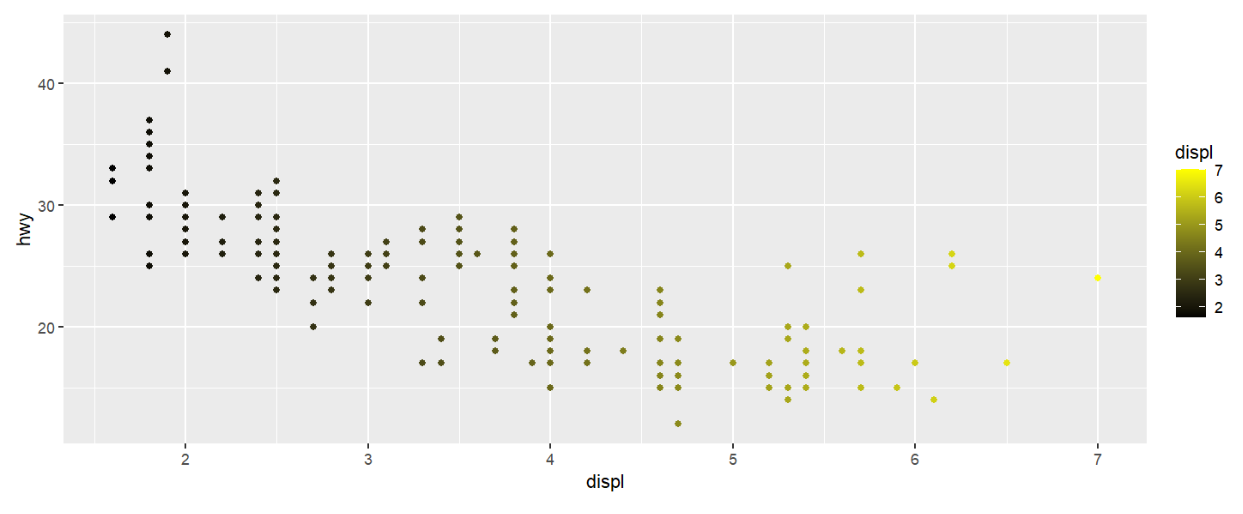
color6

该方法不需要颜色决定列为离散值，直接color=颜色决定列即可

更多种类的渐变：

scale_colour_gradient2(low=颜色1, mid=颜色2, high=颜色3, midpoint)设置颜色1->颜色2->颜色3的连续渐变，midpoint指定渐变中点对应的颜色决定列值

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( color = displ ) ) +
  scale_colour_gradient2( low = "black", mid = "red", high = "yellow", midpoint = 4.5 );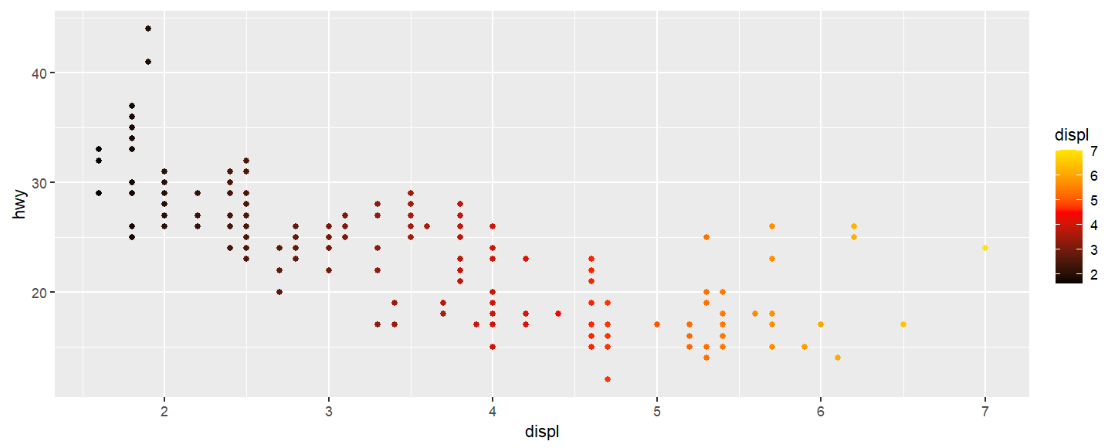

color7

scale_colour_gradientn(colors=c(颜色1, 颜色2, ...))设置更多渐变中点

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( color = displ ) ) +
  scale_colour_gradientn( colors = c("black","red", "yellow", "blue", "pink") );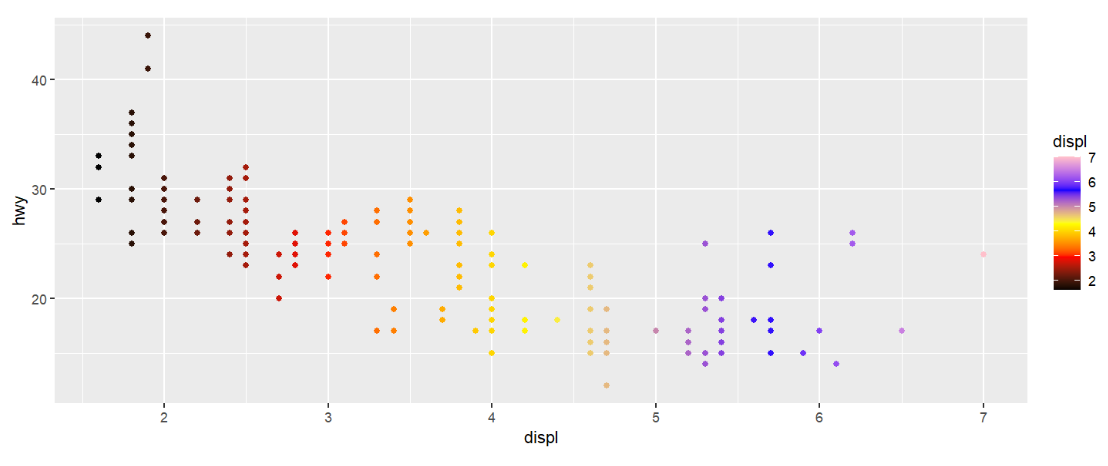

color8

即分组又渐变：scale_color_binned(low=颜色1, high=颜色2)，可以理解成非连续的渐变–一定范围内的数据被划为一组，组内数据点颜色相同，不同组的颜色构成渐变
```
mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( color = displ ) ) +
  scale_color_binned( low = "black", high = "yellow" );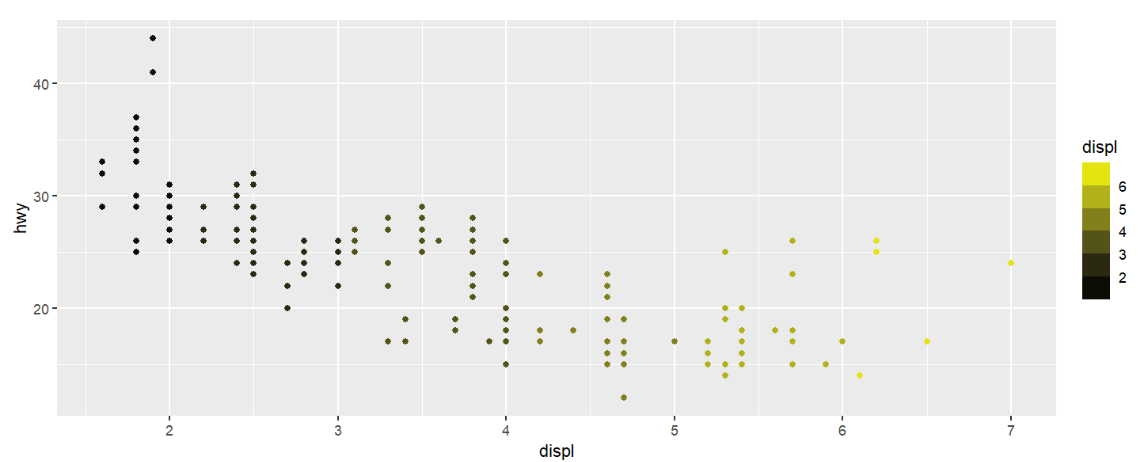
```

fill

与color的区别：fill指填充色（如果数据点可以设置填充的话），而color指边框色(stroke/outline)，它们都默认为黑色

有填充色的点：shape为21-25的点，其它点均无填充色，只有color

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( colour = cyl ), shape = 21, stroke = 2);

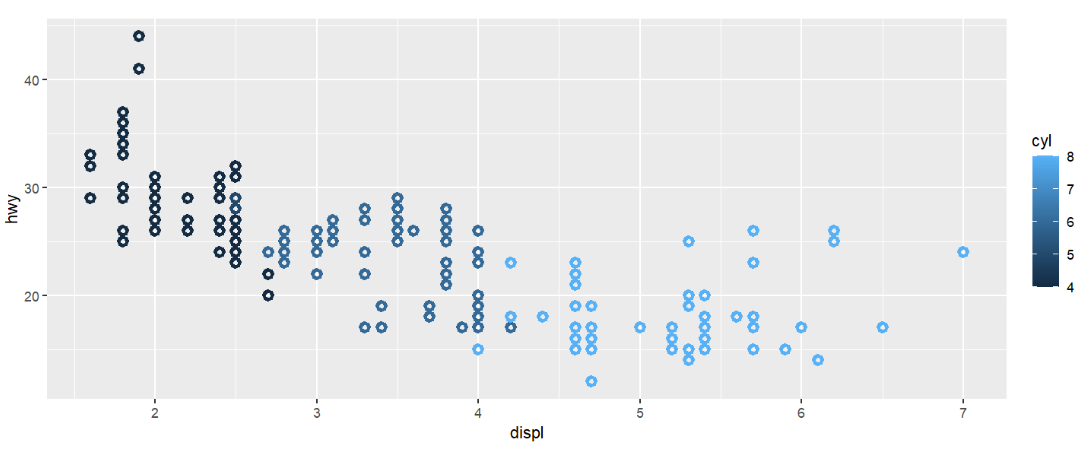
fill1

其中stroke参数指定边框线的粗细，不同与size（参数指定点的大小）

fill和color可以根据不同列来取值：

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( 
    colour = cyl,  # color根据cyl来取
    fill = class ),  # fill根据class来取
    shape = 21, size = 5,stroke = 2);

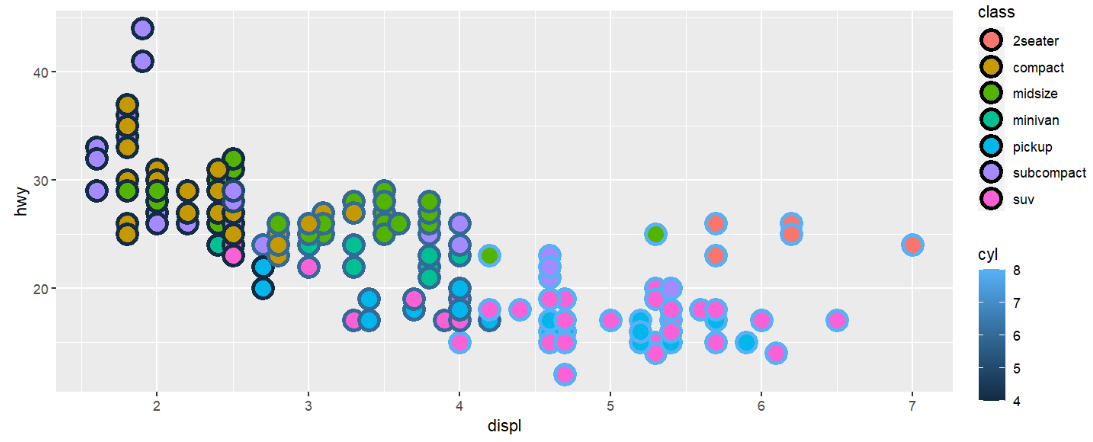
fill2

fill的色板与color相同

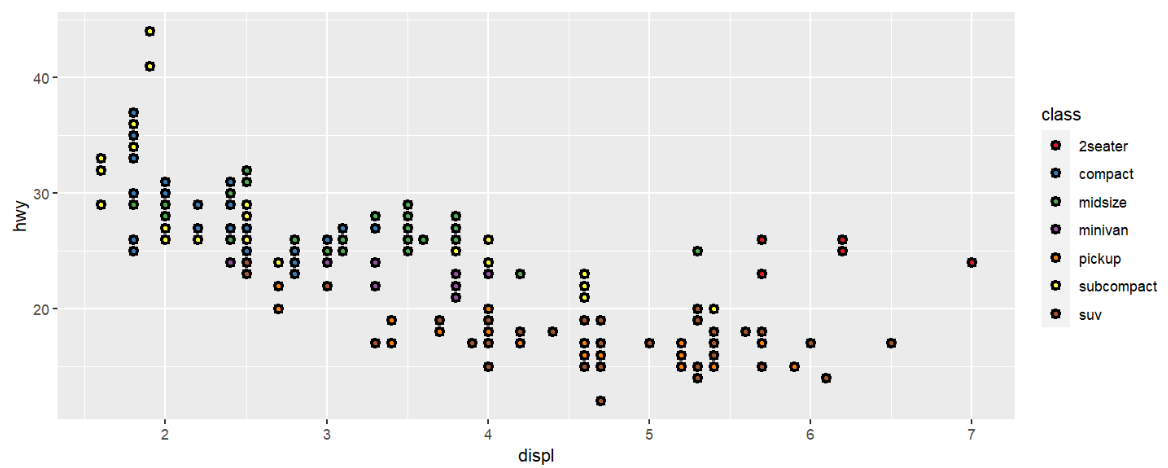
mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( fill = class ), shape = 21, stroke = 1.5) +
  scale_fill_brewer( palette = "Set1" );

fill3

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( aes( fill = cyl ), shape = 21, stroke = 1) +
  scale_fill_gradient( low = "yellow", high = "blue" ) ;

fill4

总结：

两个匹配：
- aes中的fill与函数scale_fill_xxx匹配，color与函数scale_color_xxx匹配
- 数据类型与色板类型匹配：连续数据配渐变色板，离散数据配离散色板
fill与color的色板相同，函数也通用（如scale_fill_brewer对应scale_color_brewer）
有些shape/pch只有color(stroke)，有些则两者都有

拓展：ggsci包–论文发表用的色板

if(!require("ggsci", quietly = T))
{
  install.packages("ggsci");
  library("ggsci");
}

先创建两张图：

if(!require("gridExtra", quietly = T))
{
  install.packages("gridExtra");
  library("gridExtra");
}
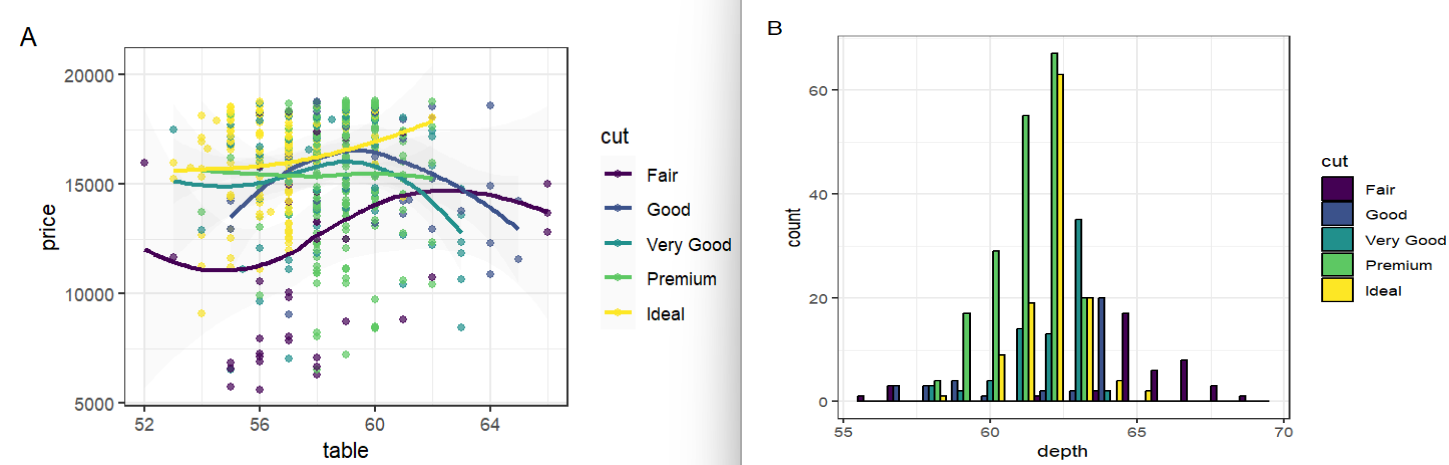
data("diamonds");
(p1 <- ggplot(
  subset(diamonds, carat >= 2.2),
  aes(x = table, y = price, colour = cut)
) +
  geom_point(alpha = 0.7) +
  geom_smooth(method = "loess", alpha = 0.05, size = 1, span = 1) +
  theme_bw() + labs( tag = "A" ));
(p2 <- ggplot(
  subset(diamonds, carat > 2.2 & depth > 55 & depth < 70),
  aes(x = depth, fill = cut)
) +
  geom_histogram(colour = "black", binwidth = 1, position = "dodge") +
  theme_bw() + labs( tag = "B" ));

fill5

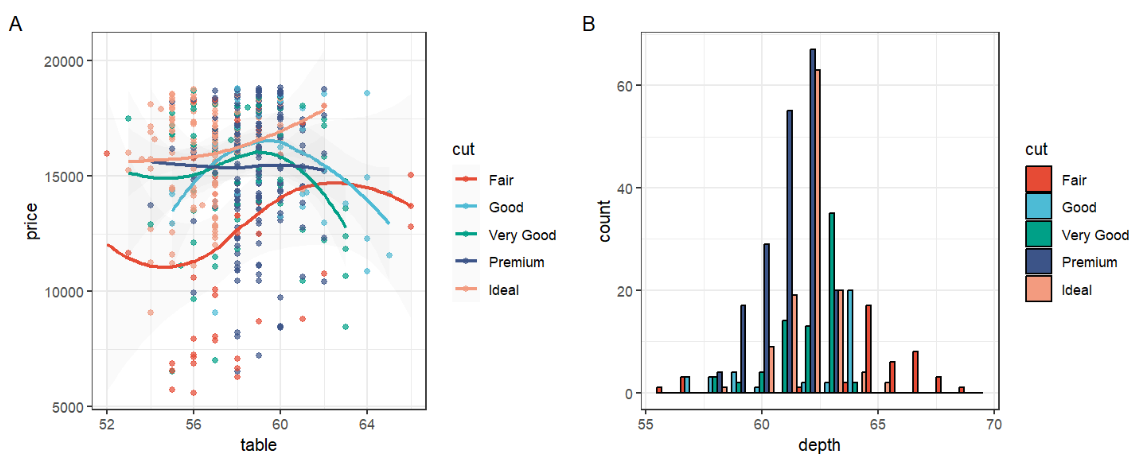
使用ggsci包中的scale_color_npg函数修改颜色：

p1_npg <- p1 + scale_color_npg()
p2_npg <- p2 + scale_fill_npg()
grid.arrange(p1_npg, p2_npg, ncol = 2)

fill6

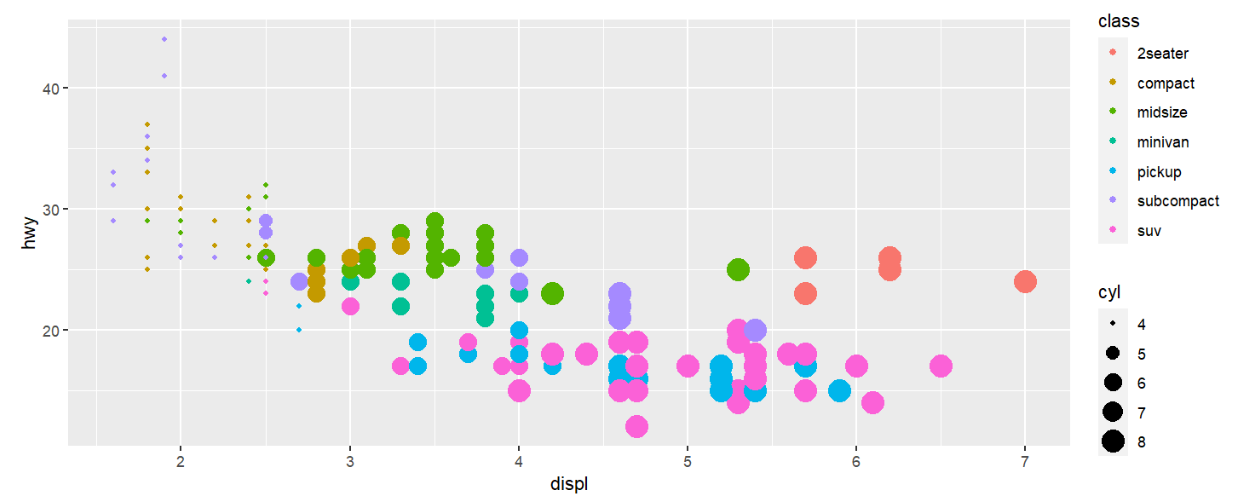
size

aes(size=列名)表示根据指定列决定点的大小

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( 
    aes( size = cyl,  # cyl列值决定点大小
         colour = class  # 点颜色由class列决定
         ) );

size

shape

aes(shape=列名)表示根据指定列决定点的大小

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( 
    aes( size = cyl,  # cyl列值决定点大小
         colour = class,  # 点颜色由class列决定
         shape = class  # class列决定点形状
         ) );

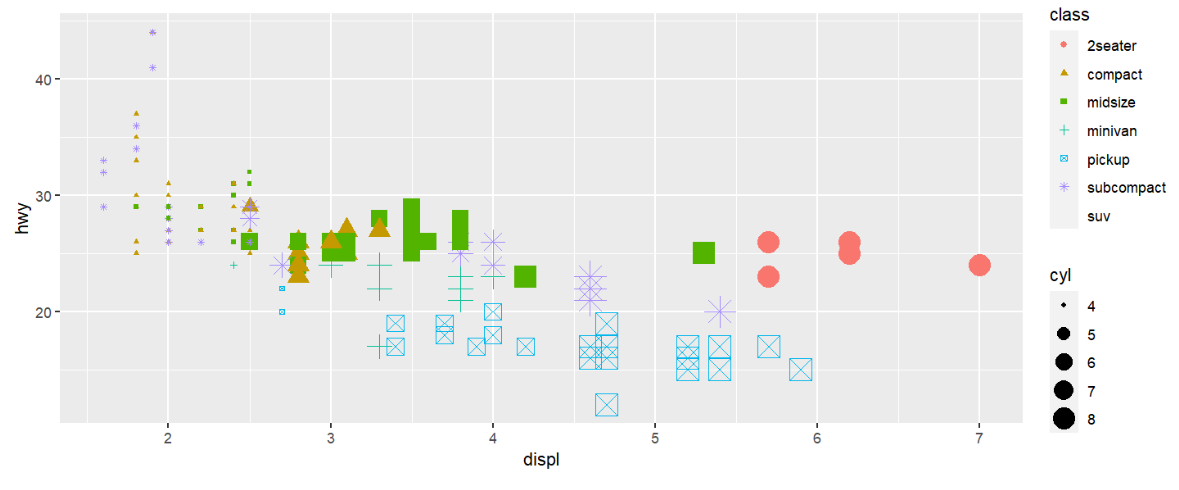
shape

总结：size、color等参数可在aes()内部，也可在外部，有什么区别？

在内部时，以指定列的值确定大小、颜色等，或按指定factor的数量确定颜色、形状的数量

在外部时，则以指定的具体值为准

mpg %>% 
  ggplot( aes(displ, hwy) ) + 
  geom_point( 
    size = 2,  # 点的大小为2
    colour = "green",  # 颜色为绿色
    shape = 21  # 形状为21号点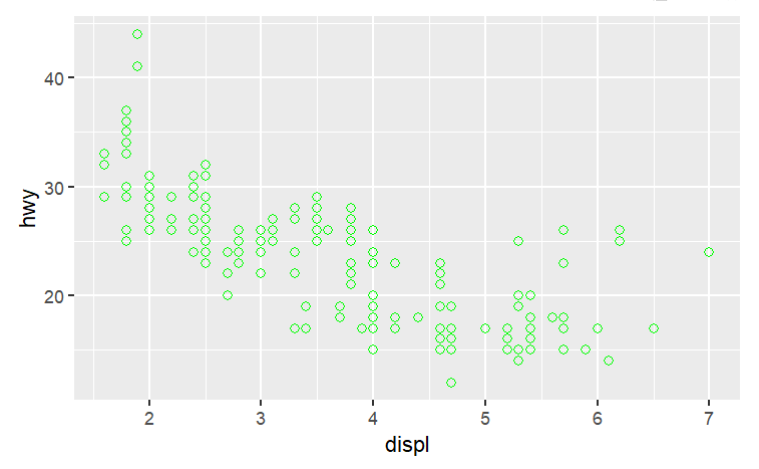
  );

shape2

可以看到所有点的大小、颜色、形状都相同

可以这样理解：size、color等参数接收的值，长度要么为1（指一个具体值，如2、'green'），要么与行数等长（一个factor或数据列）

xy轴

参考文章

为方便说明，这里只以x轴为例，y轴与x轴调整方式相同，把函数中的x换成y即可

scale_x_continuous()，适用于连续变量的坐标轴

name坐标轴名称，即坐标轴表示的是什么数据、使用什么单位等
limits坐标轴显示数据范围
breaks坐标轴刻度标签，即粗网格线，当设为NULL时无刻度
minor_breaks细网格线对应位置，细网格线没有标签
labels坐标轴刻度标签内容，默认等于breaks，是实际显示的刻度标签
position坐标轴显示位置。x轴为”left”和”right”，y轴为”top”和”bottom”
trans坐标轴变换函数，自带有”log10”、”exp”、”log2”等值
expand扩展坐标轴显示范围

例：先画基础图

(p1 <- ggplot(mpg, aes(displ, hwy)) +
  geom_point());

scale_x_continuous1

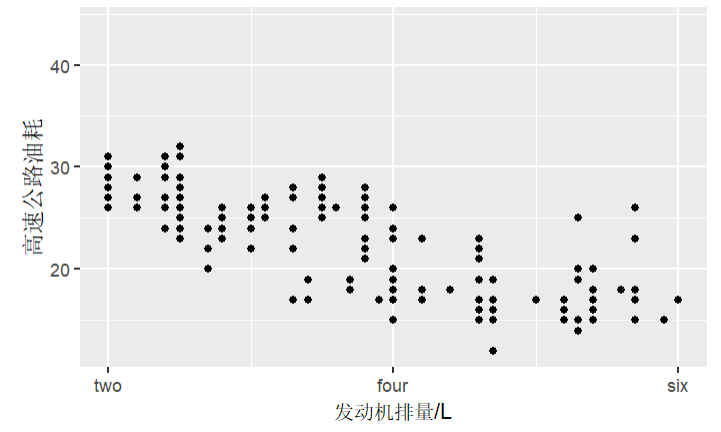
p1 + 
  scale_x_continuous(
    name = "发动机排量/L",  # 坐标轴名称
    limits = c(2,6),  # 只显示区间(2, 6)范围的元素
    breaks = c(2, 4, 6),  # 粗网格线
    minor_breaks = c(3, 5),  # 细网格线
    labels = c("two", "four", "six")  # 刻度标签
  ) +
  scale_y_continuous(name = "高速公路油耗" );  # 坐标轴名称

scale_x_continuous2

变换坐标轴：

scale_x_log10()相当于上面scale_x_continuous函数指定参数trans="log10"
scale_x_sqrt()相当于trans="sqrt"
scale_x_reverse()相当于trans="reverse"

注意：它们与scale_x_continuous都只适用于连续变量

p1 + 
  scale_x_reverse(
    name = "发动机排量/L",  # 坐标轴名称
    limits = c(6, 2),  # 只显示区间(2, 6)范围的元素
    breaks = c(6, 4, 2),  # 粗网格线
    minor_breaks = c(5, 3),  # 细网格线
    labels = c("six", "four", "two")  # 刻度标签
  );

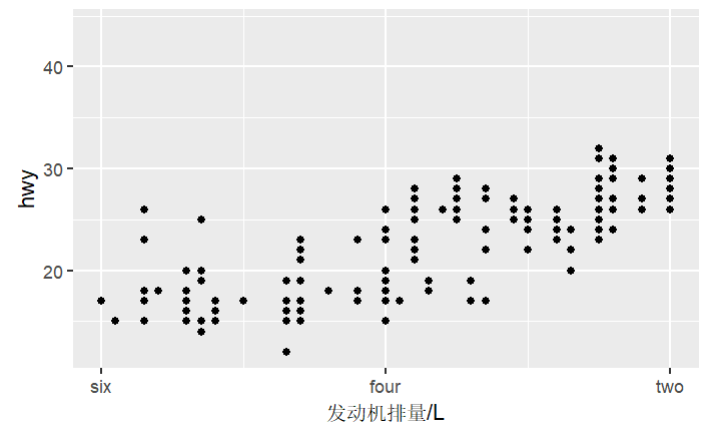
scale_x_continuous3

注意：当反转坐标轴时，要同步将limits等参数的区间设置反转，否则不会正确显示数据

scale_x_discrete()，适用于离散变量的坐标轴，参数类似于scale_x_continuous

name坐标轴名称，即坐标轴表示的是什么数据、使用什么单位等
limits坐标轴显示的数据
breaks坐标轴刻度标签，即粗网格线，当设为NULL时无刻度
labels坐标轴刻度标签内容，默认等于breaks，是实际显示的刻度标签

例：先画基础图

(p1 <- ggplot(Loblolly, aes(x = Seed, y = height)) +
  geom_boxplot(fill = "cyan"));

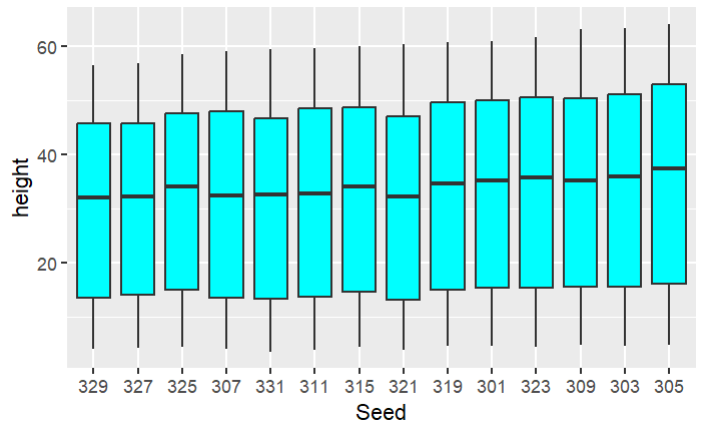
scale_x_discrete1

现要反转x坐标轴，不能使用scale_x_reverse，因为它只能用于连续变量，而上图的x轴为离散变量

ggplot(Loblolly, aes(x = Seed, y = height)) +
  geom_boxplot(fill = "orange") +
  scale_x_discrete(limits = rev(levels(Loblolly$Seed)));

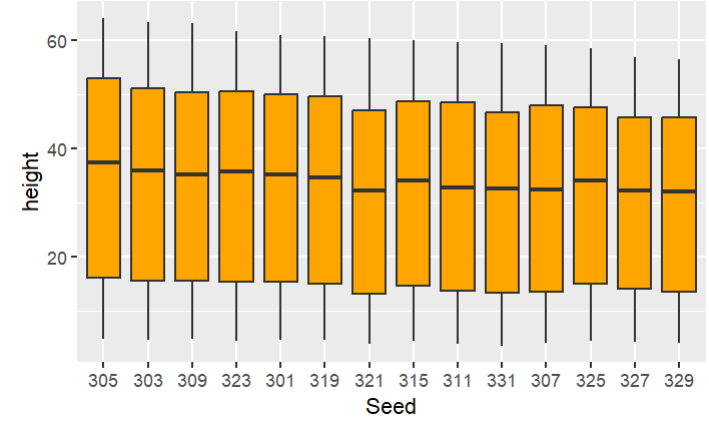
scale_x_discrete2

注意：因为Loblolly$Seed是一个factor，所以在反转它时，要使用rev(levels(Loblolly$Seed))而不是rev(Loblolly$Seed)，后者会将Loblolly$Seed按数值大小重新排序，而不是将原本的levels顺序逆序

坐标系统

线性坐标系统

coord_cartesian()：默认的坐标系统，可使用xlim、ylim等参数，指定xy轴范围，进而实现缩放局部的效果

(p1 <- ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth());

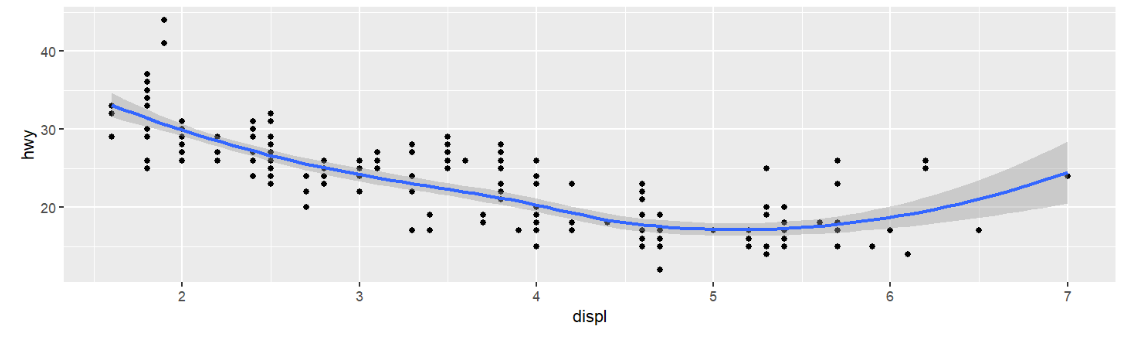
线性坐标系统1

现在想要放大x轴上4-6、y轴上10-30的部分：

p1 + 
  coord_cartesian(xlim = c(4, 6), ylim = c(10, 30));

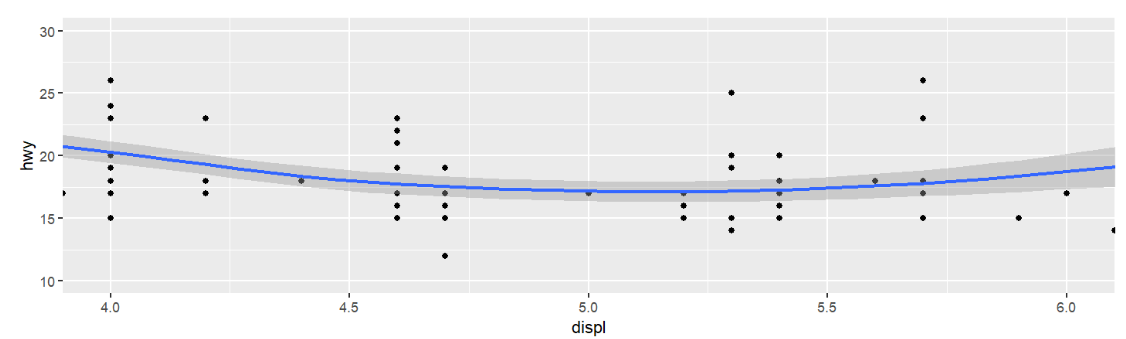
线性坐标系统2

其实就是改变了xy轴的刻度范围，刻度范围小了，图就放大了

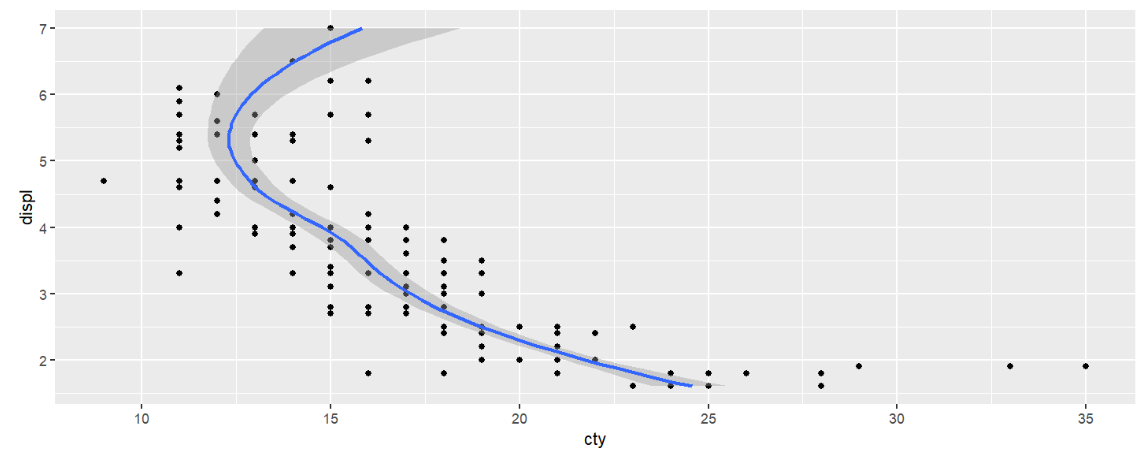
coord_flip()交换xy轴

ggplot(mpg, aes(displ, cty)) + 
  geom_point() + 
  geom_smooth() + 
  coord_flip();

线性坐标系统3

coord_fixed(radio)用特定的长宽比例(ratio)作图。长宽比例：设x轴值每增加1时，刻度向右增加的距离为n；y轴值每增加1时，刻度向上增加的距离为m，则radio=m/n

ggplot(mpg, aes(displ, cty)) + 
  geom_point() + 
  geom_smooth() + 
  coord_fixed(ratio = 1);

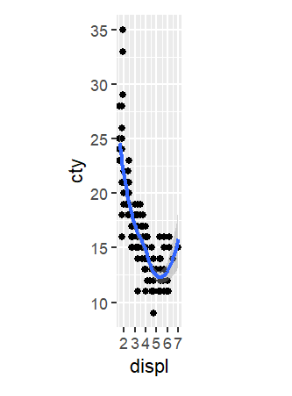
线性坐标系统4

可以看到x轴总长度(≈7)大致比y轴相邻两刻度间距(=5)略长

非线性坐标系统

coord_trans()改变xy轴刻度，并配合使用limx、limy限制xy轴的显示范围

例：先用正常的xy轴画出一条线和一个矩形

rect <- data.frame(x = 50, y = 50)
line <- data.frame(x = c(1, 200), y = c(100, 1))
(base <- ggplot(mapping = aes(x, y)) +
  geom_tile(data = rect, aes(width = 50, height = 50)) + 
  geom_line(data = line));

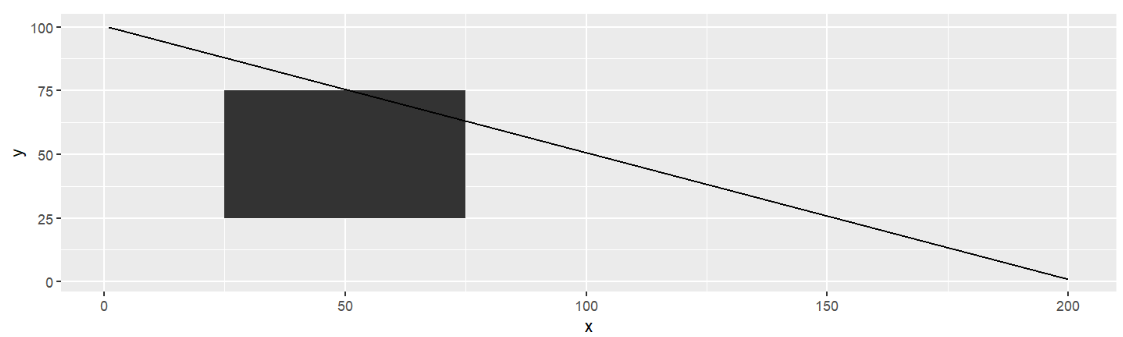
非线性坐标系统1

将y轴取log10：

base + coord_trans(y = "log10");

非线性坐标系统2

coord_polar()将指定的轴变为圆形，画极坐标图

base + coord_polar();  # 默认为 coord_polar("x")
base + coord_polar("y");

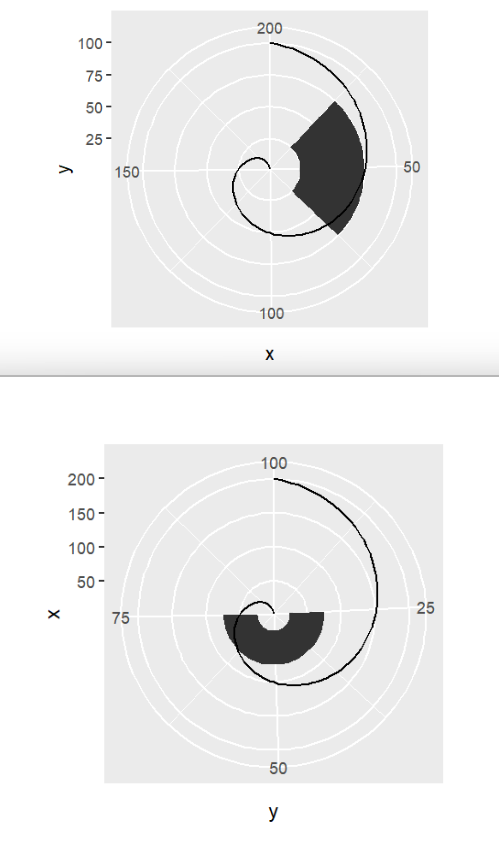
非线性坐标系统3

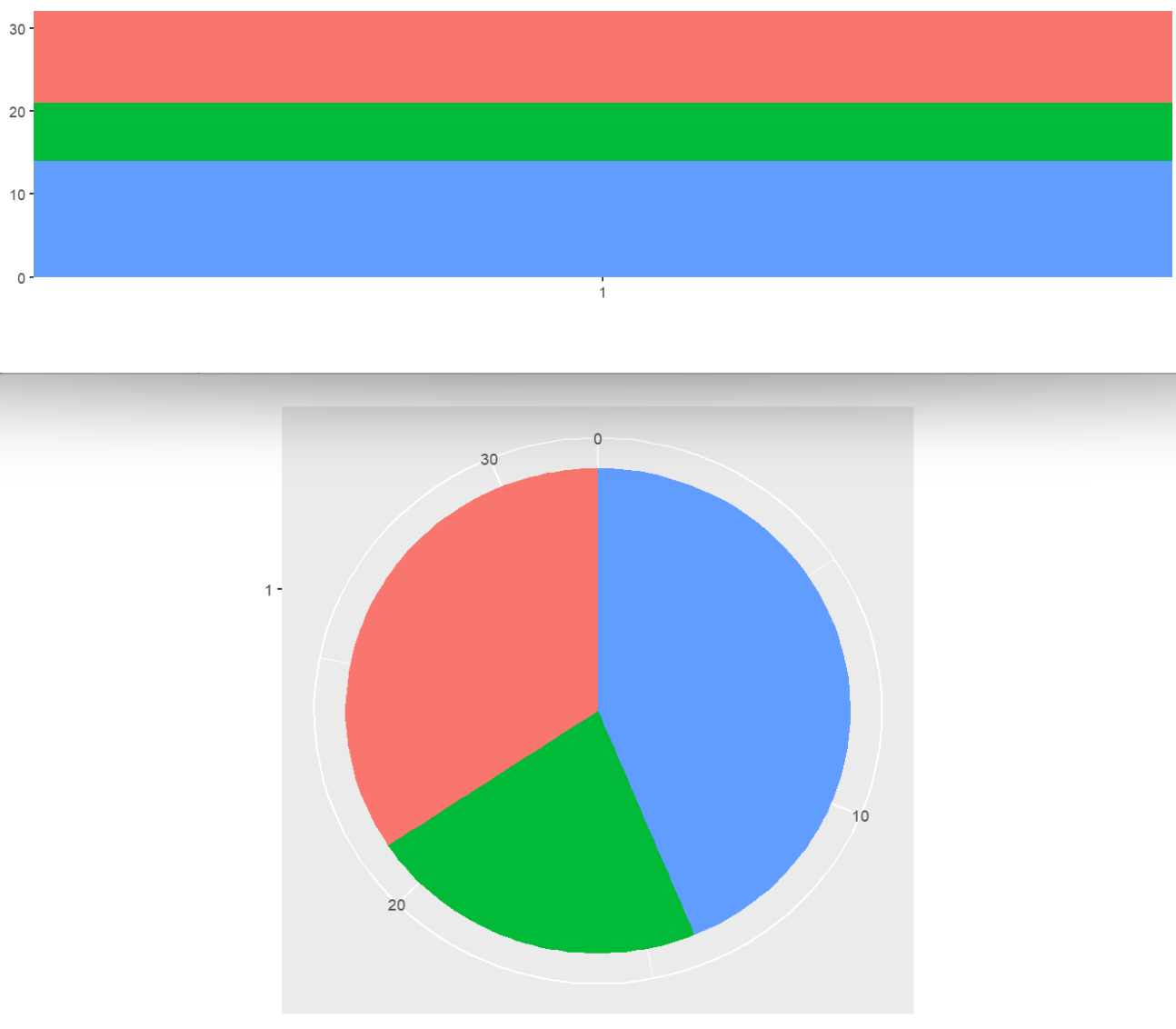
还可以用于将柱形图变成饼图：

(base <- ggplot(mtcars, aes(factor(1), fill = factor(cyl))) +
  geom_bar(width = 1) + 
  theme(legend.position = "none") + 
  scale_x_discrete(NULL, expand = c(0, 0)) +
  scale_y_continuous(NULL, expand = c(0, 0)));
base + coord_polar(theta = "y");  # 变饼图

非线性坐标系统4

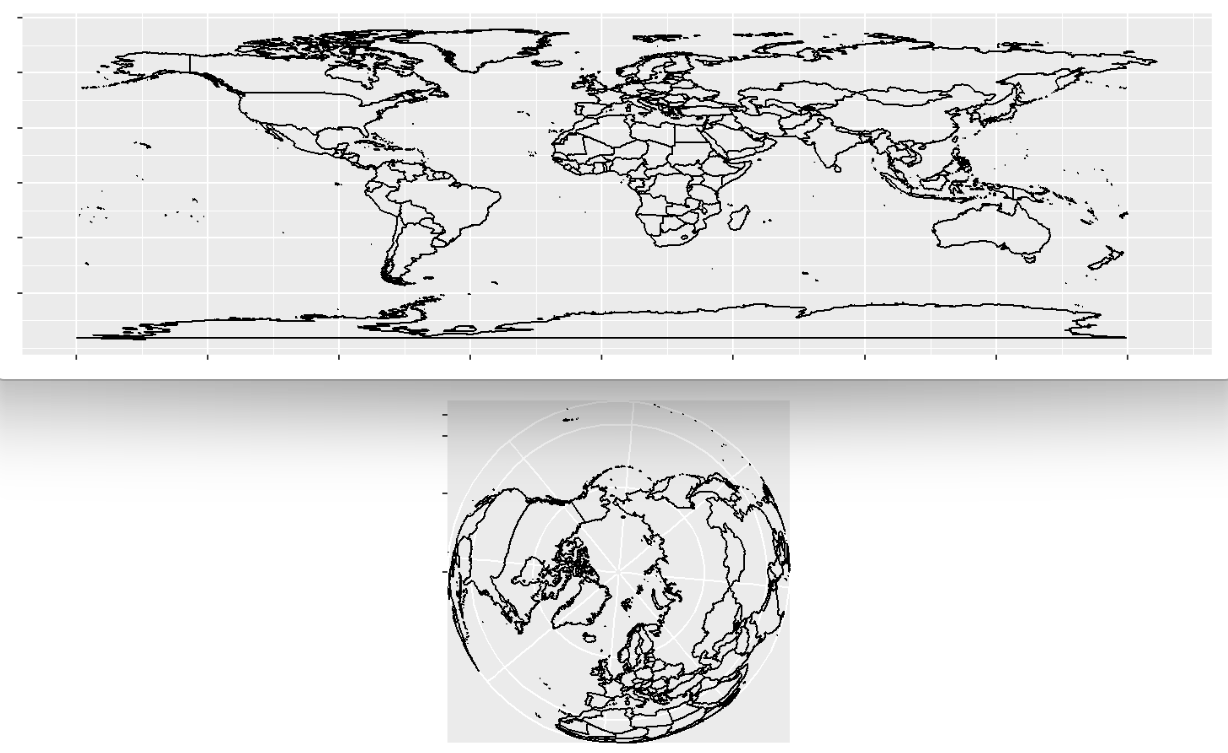
coord_map()用于将矩形地图变成圆形的

world <- map_data("world")
(worldmap <- ggplot(world, aes(long, lat, group = group)) +
  geom_path() +
  scale_y_continuous(NULL, breaks = (-2:3) * 30, labels = NULL) +
  scale_x_continuous(NULL, breaks = (-4:4) * 45, labels = NULL));
if(!require("mapproj", quietly = T))
{
  install.packages("mapproj");
  library("mapproj");
}
worldmap + coord_map("ortho");

非线性坐标系统5

faceting画子图

facet_grid(by_row ~ by_col)按by_col列分成多列，或按by_row列分成多行，之后每行/每列画一个子图

ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() +
  facet_grid( . ~ cyl, scales = "free" );  # 按cyl分成三列
ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() +
  facet_grid( cyl ~ . )  # 按cyl分成三行

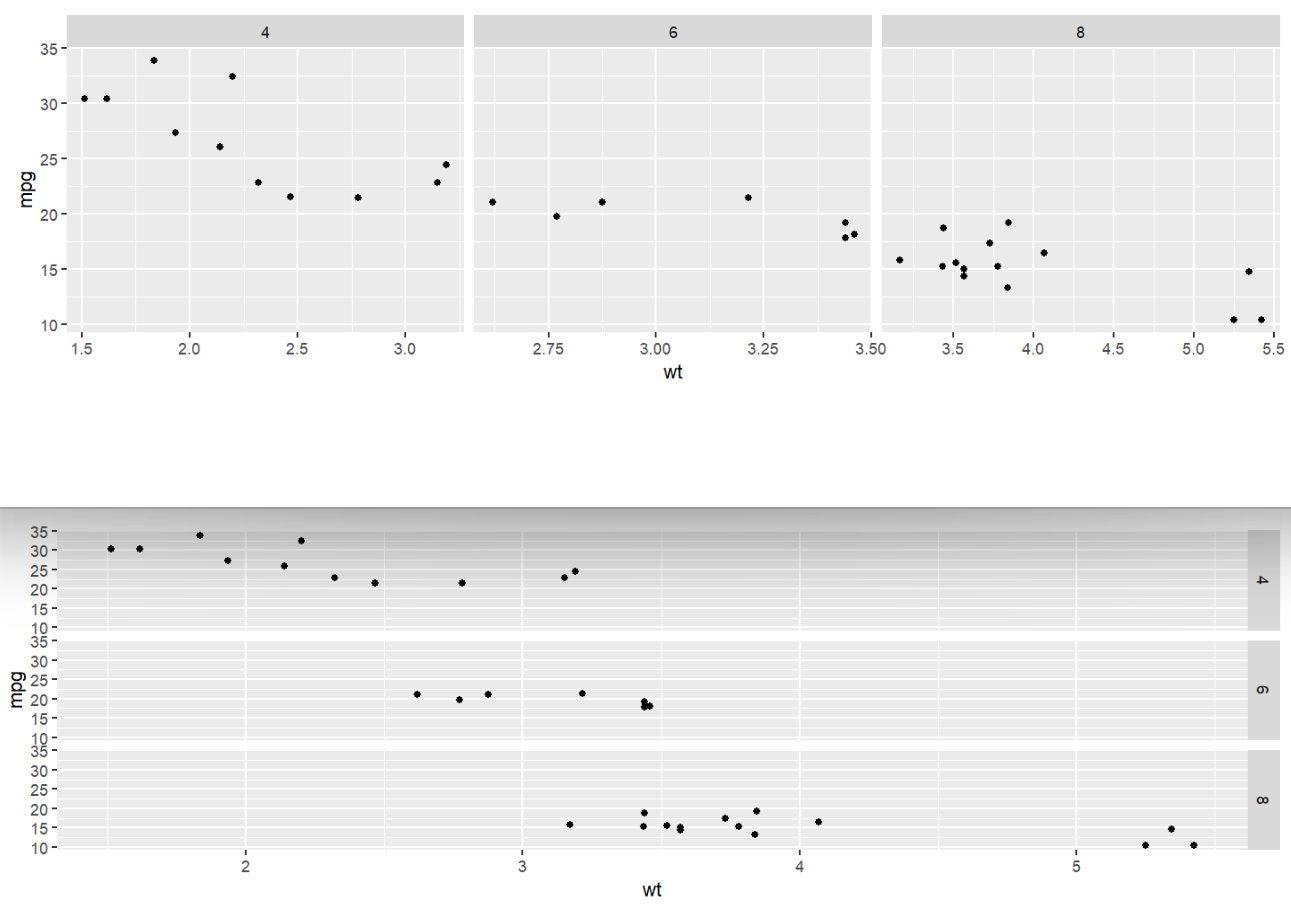
faceting1

默认情况下，如果指定分成多列，则所有子图有相同的xy范围。可以设置scales = "free"参数，使子图仅有相同的y轴，x轴范围根据每个子图的数据不同。（指定分成多行的情况类似）

ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() + 
  geom_smooth( method = "lm" ) +  # 向散点图中添加拟合曲线
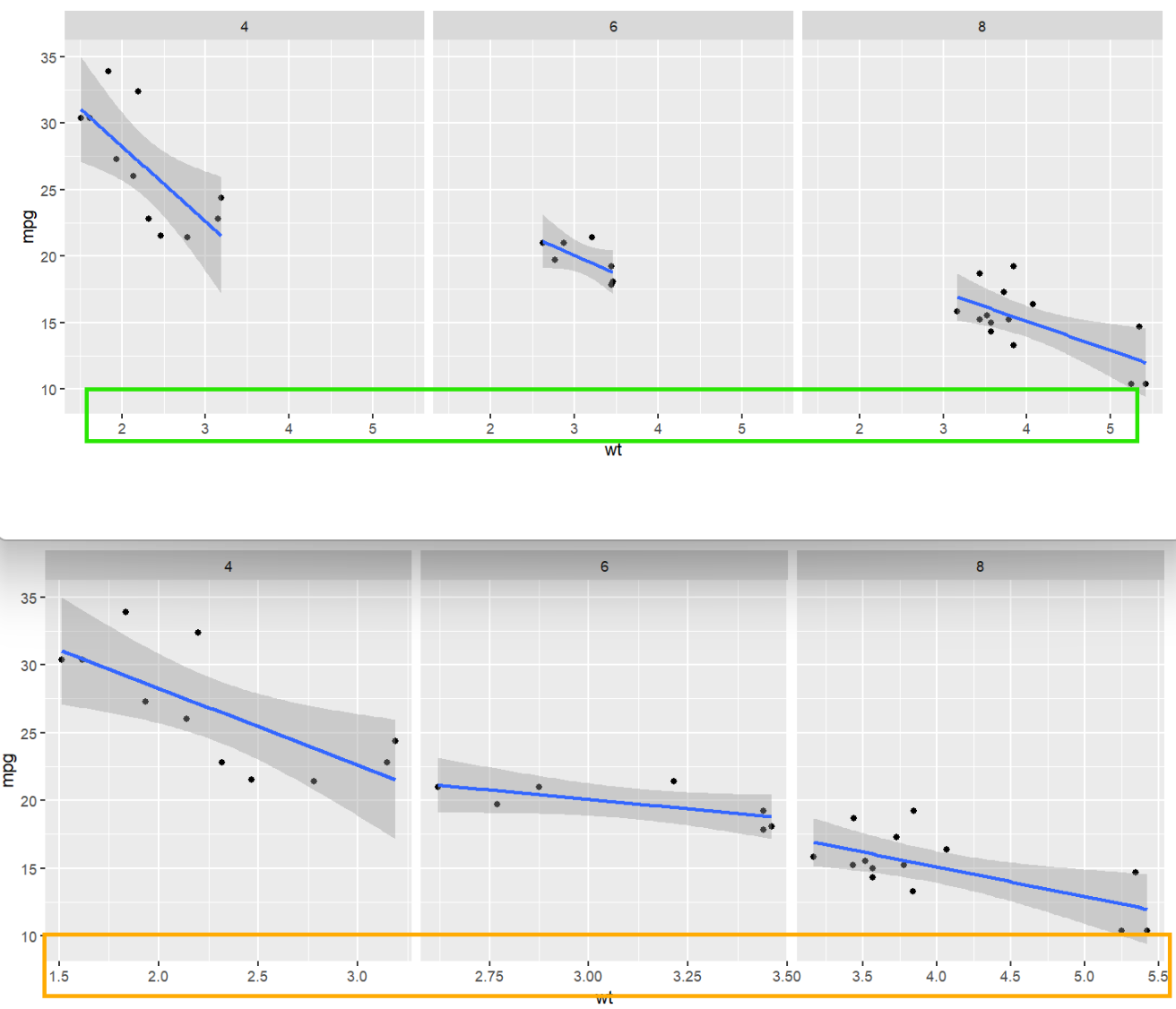
  facet_grid( . ~ cyl );  # 此时x轴是共享的，用同一个x轴
ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() + 
  geom_smooth( method = "lm" ) + 
  facet_grid( . ~ cyl, scales = "free");  # 根据每张图的数据范围确定x轴范围

faceting2

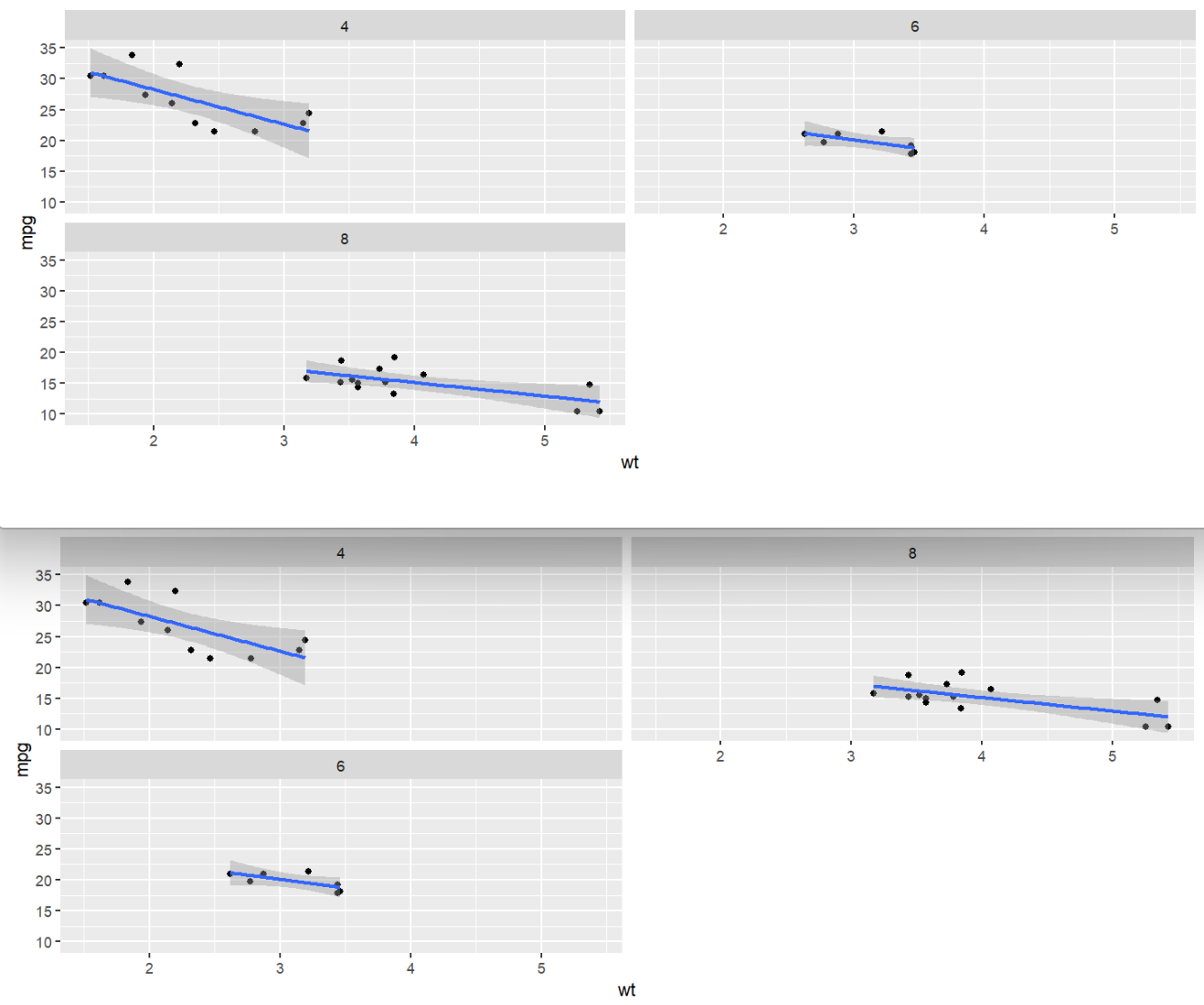
facet_wrap(by_row ~ by_col, ncol, nrow)与前面facet_grid类似，都是按指定列画子图，不同的是，它可以指定画成几列/行，让每列/行有多个图

ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() + 
  geom_smooth( method = "lm" ) + 
  facet_wrap( . ~ cyl , ncol = 2);  # 共有两列
  # 也可以写成：
  # facet_wrap( cyl ~ . , ncol = 2);
ggplot( mtcars, aes( x = wt, y = mpg ) ) +
  geom_point() + geom_smooth( method = "lm" ) + 
  facet_wrap( . ~ cyl , ncol = 2, dir = "v" );  # dir指定第二个子图是往下还是往右画，默认往右

faceting3

统计与绘图

基本统计类生成函数

正态分布：norm系列函数

rnorm(10000, mean = 0, sd = 1)生成10000个平均值为0、标准差为1的数据（标准正态分布）

(mean + 1 * sd)包含68%的数据
(mean + 2 * sd)包含95%的数据
(mean + 3 * sd)包含99%的数据

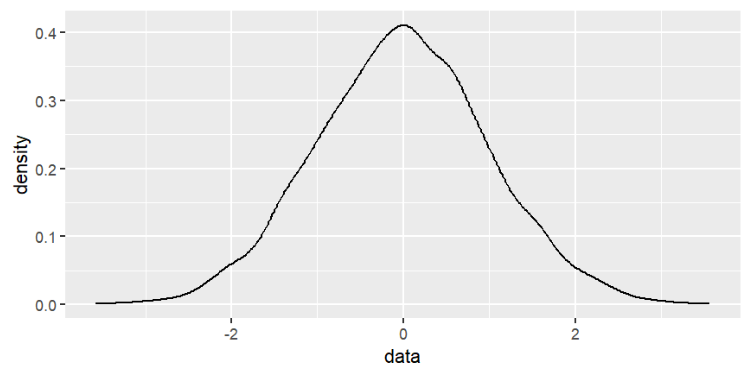
x <- rnorm(10000, mean = 0, sd = 1);
ggplot( data.frame( data = x ), aes( data ) ) + 
  geom_density();  # 密度图--显示数据的分布情况

统计类函数1

其它norm系列函数：

dnorm(x, mean, sd)正态分布的概率密度函数(pdf)
pnorm(x, mean, sd)正态分布的累积密度函数(cdf)
qnorm(x, mean, sd)正态分布的逆累积密度函数

均匀分布：runif(10000, min = 0, max = 1)生成10000个均匀分布在0-1间的数据

x <- runif( 10000 );  # 默认均匀分布在0-1
ggplot( data.frame( dat = x ), aes( x ) ) + 
  geom_histogram();  # 直方图--显示各区间的数据多少

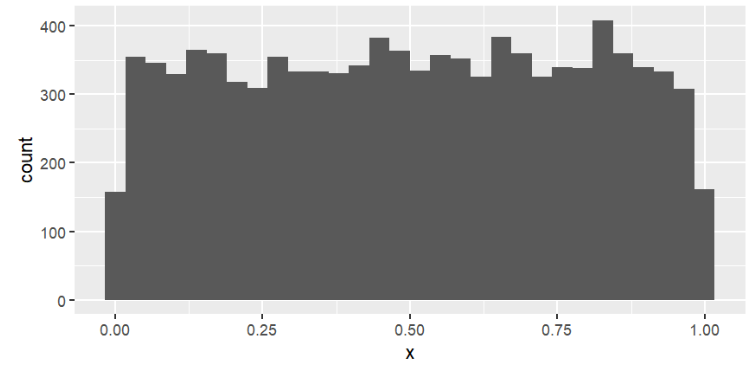
统计类函数2

其它统计类生成函数：

rbinom(x, 试验次数size, 每次试验的成功概率prob)二项式分布
rpois(n, lambda)泊松分布，体现在特定时间内发生n个事件的概率
rexp(n, rate)指数分布，体现一个随机事件发生需要的时间
rgamma(n, shape)伽马分布，体现n个随机事件都发生需要的时间

将它们绘制出来：

n <- 10000;
uni <- tibble( dat = runif(n), type = "uni" );
norm <- tibble( dat = rnorm(n), type = "norm" );
binom <- tibble( dat = rbinom(n, size = 100, prob = 0.5), type = "binom" );
poisson <- tibble( dat = rpois(n, lambda = 4), type = "poisson" );
exp <- tibble( dat = rexp(n, rate = 1) , type = "exp");
gamma <- tibble( dat = rgamma(n, shape = 1) , type = "gamma");
combined <- bind_rows( uni, norm, binom, poisson, exp, gamma );
ggplot( combined , aes( dat ) ) + geom_density() +
      facet_wrap( ~type, ncol = 3, scales = "free");

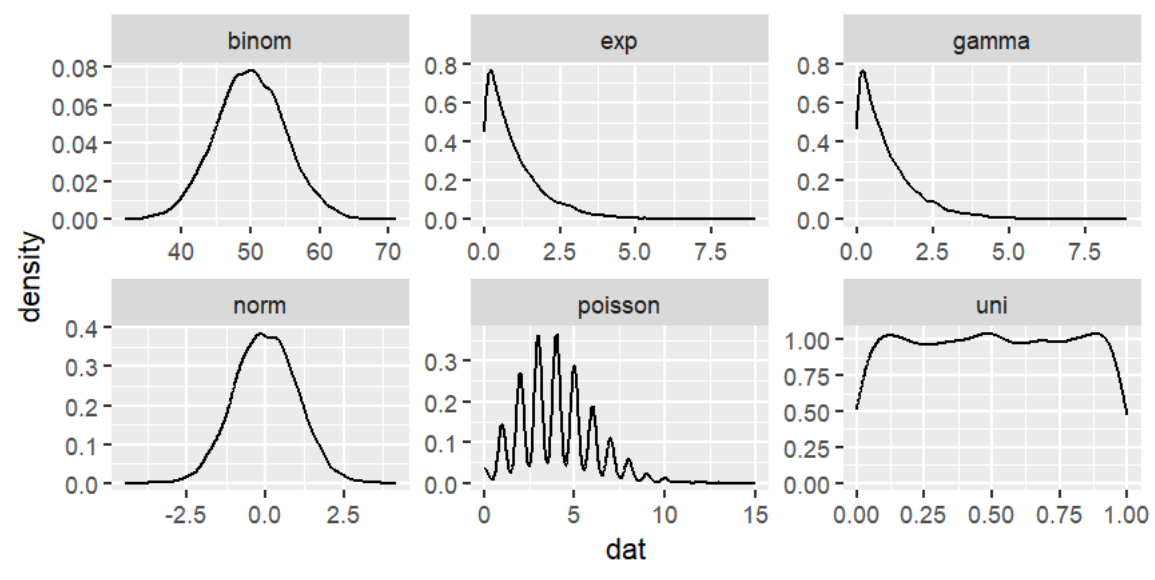
统计类函数3

常用量化描述函数

mean平均值
median中值
sd标准差
var样本方差
range最大值和最小值
quantile分位值
summary(data)
- 当data为数值型数组时：计算最大最小值、1/3分位值、平均值、中值
- 字符型数组：长度、类型

num <- c(1, 2, 3, 3, 4, 5, 5);
str <- c("uni", "norm", "binom", "poisson", "exp", "gamma");
mean(num);  # 3.285714
median(num);  # 3
sd(num);  # 1.496026
var(num);  # 2.238095
range(num);  # 1 5

quantile(num);#分位值

  0%  25%  50%  75% 100% 
 1.0  2.5  3.0  4.5  5.0 

summary(num);

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   2.500   3.000   3.286   4.500   5.000 

summary(str);

   Length     Class      Mode 
        6 character character 

quantile还能指定计算哪几个分位点

quantile(num, probs = seq(0, 1, length = 11));

表示计算0%-100%之间共11个分位点，即每隔10%计算一次

  0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
 1.0  1.6  2.2  2.8  3.0  3.0  3.6  4.2  4.8  5.0  5.0

table函数：数组中有哪些值和它们的出现次数

num <- c(1, 2, 3, 3, 4, 5, 5);
table(num);

num
1 2 3 4 5 
1 1 2 1 2 

也可以接收一个df：table(df$a, df$b)先按a列分组，再计算每组中b列中每个值的出现数量，默认按第一列分组

参考文章

常用量化描述函数2

常用量化描述函数3

count相关函数：

dplyr::count(data, 分组列)现按分组列分组，之后计算每组的数量（其实就是分组列中各元素数量）

例：使用基本统计类生成函数最后面创建的combineddf

# 这两种方法结果相同
combined %>% count( type );
combined %>% group_by(type) %>% count();

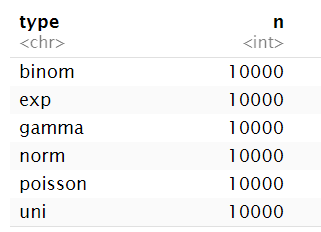
常用量化描述函数4

可以有多个分组列：

# 这两种方法结果相同
iris %>% 
  group_by(Species) %>% 
  count(Petal.Width);
iris %>% count(Species, Petal.Width);

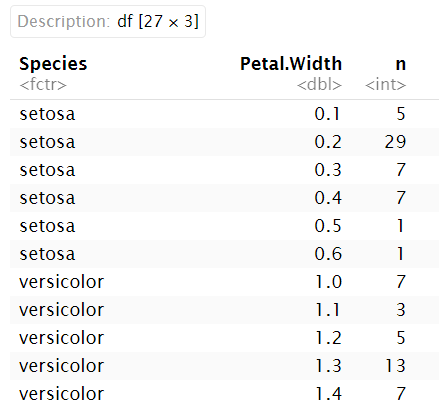
常用量化描述函数5

各种数据及所画的图

数值+分组–箱型图

即一列是数值，另一列是分组信息的数据

data.fig3a <- read_csv( file = "r-data/nc2015_data_for_fig3a.csv" );  # 读取数据
head( data.fig3a[ c("tai", "trans.at") ] );  # 只显示有用的两列

箱型图1

tai：基因表达量的一种计算方式，从1到5表达量逐渐升高
trans.at：基因中A碱基数量减去T碱基数量

假设：A的在生物体内的合成成本高于T，因此高表达基因在可能的情况下倾向于使用T而不是A。因此，在高表达的基因当中，A-T的差值trans.at会变大（更负）

为了验证这个假设，需要画箱型图geom_boxplot

x轴数据为tai，y轴数据为trans.at

注意：我们需要每个tai都画一个箱型图，此时需要factor(tai)，类似于分组操作；如果直接输入tai，则只能画出一个箱型图（包含所有的数据）

fig3a <- 
   ggplot( data.fig3a, aes( factor(tai), trans.at ) ) +  # 输入数据
   geom_boxplot( fill = "#22AD5C", linetype = 1 ,outlier.size = 1, width = 0.6) +  # 画箱型图
   xlab( "tAI group" ) +  # x轴标签
   ylab( expression( paste( italic(S[RNA]) ) ) ) +  # y轴标签
   scale_x_discrete(breaks= 1:5 , labels= paste("Q", 1:5, sep = "") ) +  # 指定x轴标签
   geom_hline( yintercept = 0, colour = "red", linetype = 2);  # 在y=0的位置添加标注线
fig3a;

箱型图2

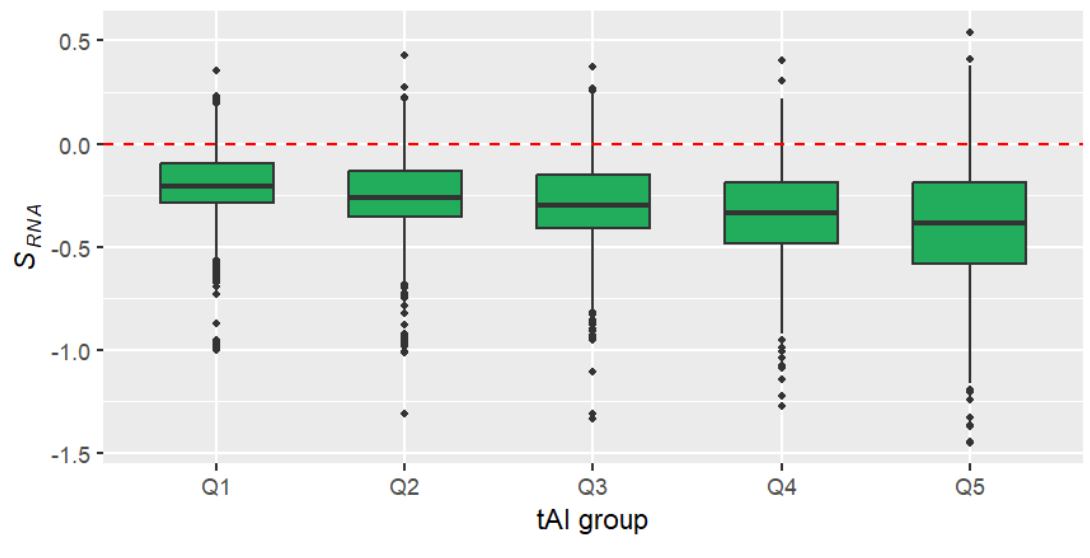
一般情况下，我们只看中值的变化趋势，即箱型图最中间的那条线，可以看到从Q1->Q5trans.at中值依次下降，说明假设是正确的

也可增加Q1-Q5之间的差异分析来辅助说明假设正确性

使用geom_signif包：

if (!require("geom_signif")){ 
  install.packages("geom_signif");
  library("geom_signif");
} 

fig3a + geom_signif( 
  comparisons = list(1:2, 2:3, 3:4, 4:5),   # 第1和2组数据比较、第2和3组数据比较...
  test = wilcox.test,  # 检测方法
  step_increase = 0.1 );  # 让结果数值分开（下一组比上一组结果高0.1个单位）

箱型图3

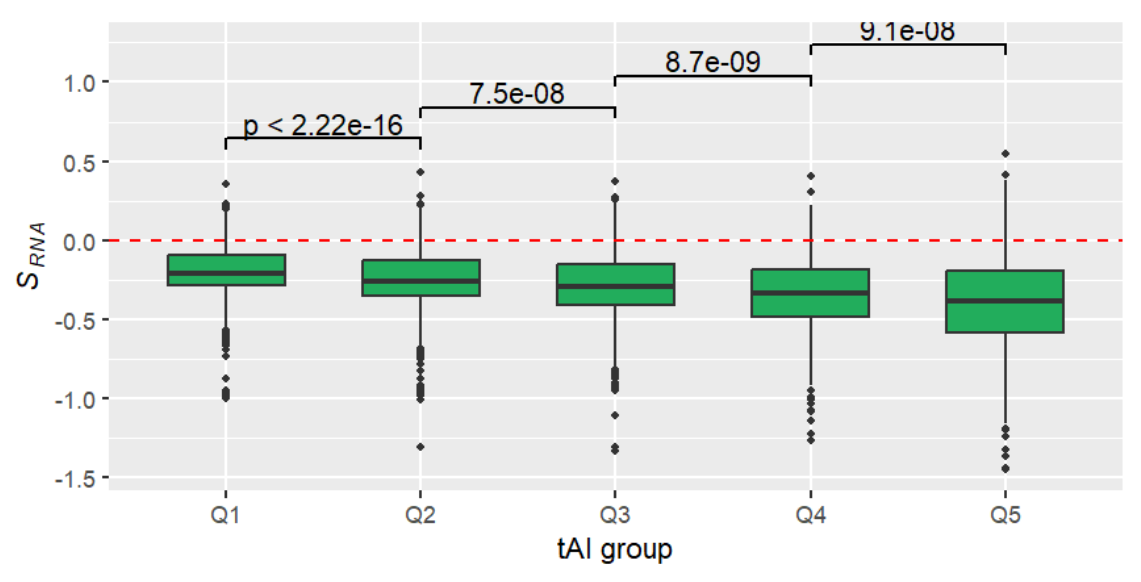
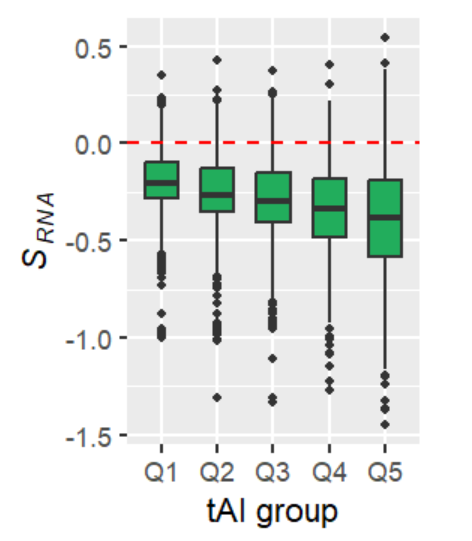
一般情况下，我们画出的箱型图要高瘦，而不要矮胖。可以使用Rmd中代码框自带的fig.height/fig.width属性修改：

{r fig.height=2.5, fig.width=2}
fig3a;  # 更改fig.height/fig.width的值

箱型图4

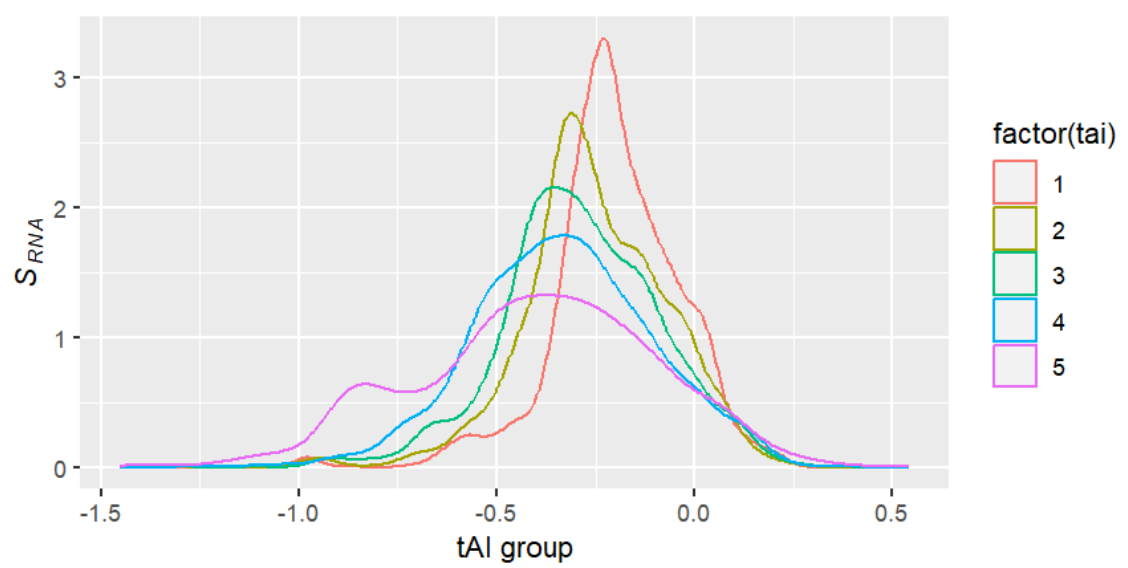
这种数据也可以使用直方图(density plot)，但在此例中不如箱型图

ggplot( data.fig3a, aes( trans.at, colour = factor(tai) ) ) + 
  geom_density( ) +  # 直方图
  xlab( "tAI group" ) + 
  ylab( expression( paste( italic(S[RNA]) ) ) );

箱型图5

多组数值–散点图

即有两列或多列为数值型的数据，通常我们想要知道两组数据间的关系，或者说一组数据受另一组数据的影响

以mtcars为例：

多组数值1

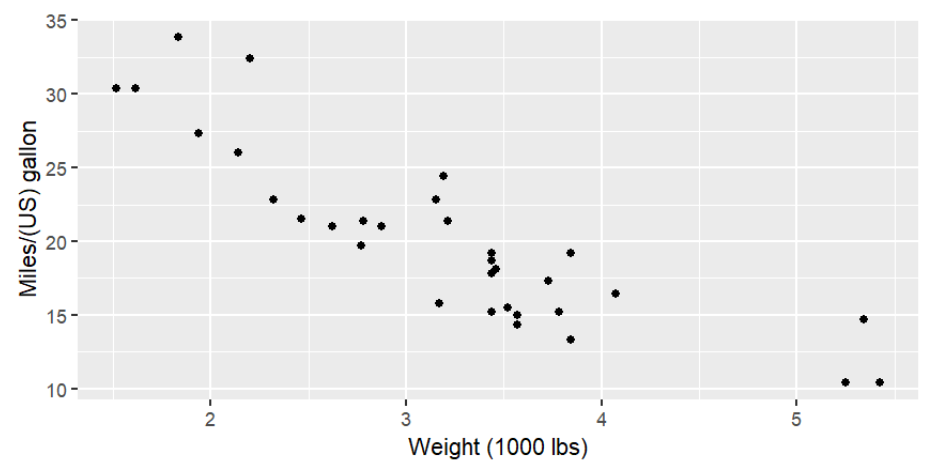
查看重量wt与燃油效率mpg之间的关系：

plotcars <- 
  ggplot( mtcars, aes( x = wt, y = mpg ) ) + 
  geom_point() + 
  xlab( "Weight (1000 lbs)" ) + 
  ylab( "Miles/(US) gallon" );
plotcars;

多组数值2

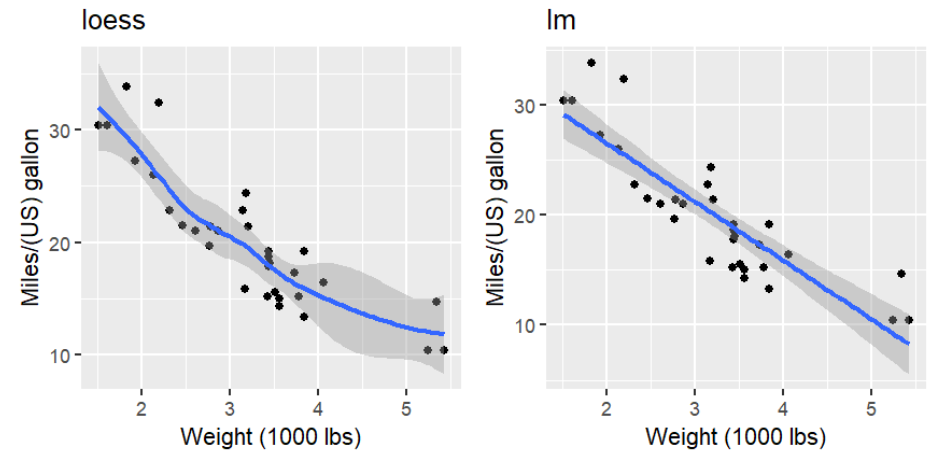
使用geom_smooth添加拟合线：

loess <- plotcars + geom_smooth() +  # 拟合曲线（默认值）
  ggtitle("loess");
lm <- plotcars + geom_smooth( method = "lm" ) +  # 线性回归（直线）
  ggtitle("lm");
if (!require("cowplot")){ 
  install.packages("cowplot");
  library("cowplot");
} 
cowplot::plot_grid(loess, lm, ncol=2);

多组数值3

多组数值–箱型图

当趋势不明显时，可以按另一组数据分组

通常有两种分组方法：

等距分组(equal-distance binning)：取最大最小值，分为多个距离相等的区间，把数据值在相同区间的行分为1组
等频分组(equal-size binning)：确保每组的数量相同，每组的距离不一定相等

等频分组使用ntile(data, n)，表示将数据分成n组，每组的数据量相同

等距分组使用cut(data, break)，breaks接收一个数字型vector(a,b,c...)，表示按(a-b]、(b-c]、(c-…]进行分组

注意cut函数不仅用于等距分组，还可以指定任意距离进行分组。更多关于cut函数

mtcars2 <- mtcars %>% 
   mutate( 
     group1 = ntile( wt, 4 ),  # 等频分组
     group2 = cut(
       wt, 
       breaks = seq( from = min(wt), to = max(wt), by = (max(wt) - min(wt)) / 4 ),  # 表示平均分成
       include.lowest = T 
   )  # 等距分组 
);
mtcars2;

多组数值4

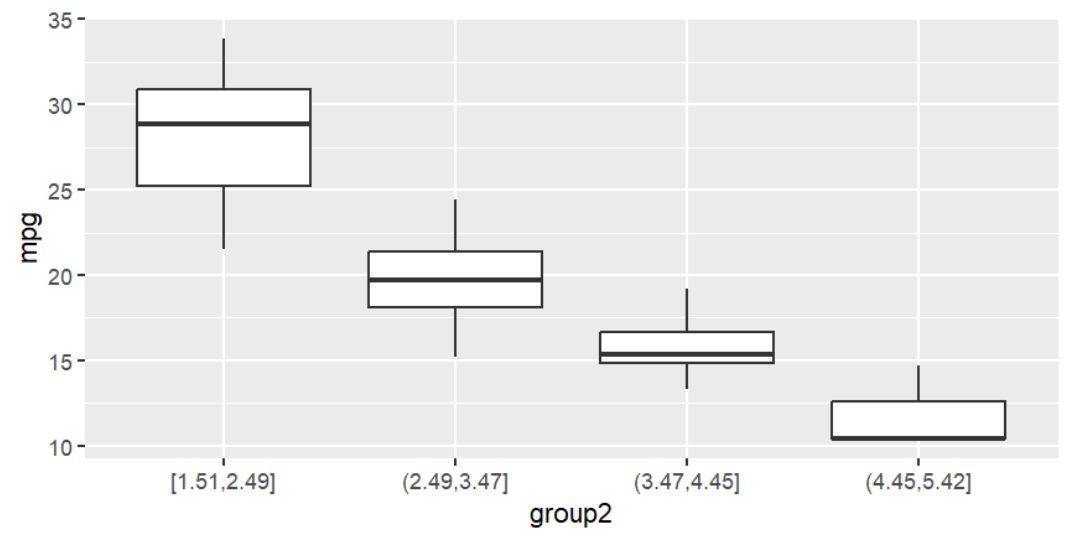
等频分组结果：

table( mtcars2$group1 );

1 2 3 4 
8 8 8 8 

表示共有1234共4组，每组都有8个数据

等距分组结果：

table( mtcars2$group2 );

[1.51,2.49] (2.49,3.47] (3.47,4.45] (4.45,5.42] 
          8          13           8           3 

第一行是分组的区间，第二行是每组个数，可以看到区间距离相等而每组个数不相等

使用箱型图描述分组结果：

ggplot( mtcars2, aes( group2, mpg ) ) + 
   geom_boxplot();

多组数值5

统计学中的各种检验

一些统计学概念

主要参考文章

零假设(null hypothesis)：假定为真的某种假设，通常表达为总体参数等于某个固定值。例如，“这个群体的平均年龄是50岁”、“这个药物对治疗癌症没有作用”等等

非零假设(alternative hypothesis/non-null hypothesis)：零假设的对立。例如零假设是“两组数据没有区别”，非零假设就是“两组数据有区别”

P值(P value)；在零假设成立的条件下，观察到当前统计量或更极端统计量的概率，用于评估观察到的数据与零假设下期望的数据之间的差异

较低的P值意味着观察结果与零假设下的期望结果差异很大。通常，如果P值低于预定的显著性水平（如0.05），我们会认为零假设不成立，而非零假设成立

可以简单理解为：基于零假设，观察到某种情况发生的可能性有多大。这个概率越小，零假设错误的可能性就越高

P value summary：是一种简洁的方式来表示P值的大小

***: P < 0.001
**: 0.001 ≤ P < 0.01
*: 0.01 ≤ P < 0.05
.: 0.05 ≤ P < 0.1
` `（空格）: P ≥ 0.1

“一尾”和“双尾”P值：

双尾P值
- 如果在做假设检验时，没有预期的方向或者对两个方向都感兴趣，则应进行双尾测试
- 例如，想知道药物A是否与药物B有不同效果（不管是更好还是更差），这个假设包含了两个方向（更好/更差）
- 给出了观察数据在零假设下出现的概率，不考虑方向
一尾P值
- 当预期了某个方向的效果时，应进行一尾测试
- 例如，想知道药物A是否比药物B更好时（而不是更差）
- 给出了在特定方向上观察到的数据在零假设下出现的概率
比较
- 一尾P值通常是双尾P值的一半
- 选择一尾还是双尾测试应该基于研究问题和假设，而不是基于数据
- 应谨慎使用一尾测试，因为它更容易发现在预期方向上的效应，但同时更可能忽略另一个方向上的真实效应

t值：表示了样本数据与零假设之间的差异大小

自由度(Degrees of Freedom/df)：反映数据中可用于估计参数的独立信息量的值，用于确定t值的显著性水平

在独立样本T检验中，通常是两个样本的总样本量减去2。例如，如果有两个样本，每个样本有10个观测值，那么df = (10 + 10) - 2 = 18
在配对样本或单样本T检验中，自由度是样本量减去1

t-test：常用于检验样本与假设的均值差异。比如单样本时，检验样本均值是否等于某一数值；双样本时，检验两个样本的均值是否相等

要求：两个样本需来自呈正态分布的总体、方差需相等

应用：

paired-sample：检验配对的样本之间的均值差异。比如同一组样本的两次测量结果之间的比较，又比如临床试验中两组年龄和性别上不同的样本
independent sample：随机的两个样本之间的均值检验。比如检验两个班的月考数学成绩

95%置信区间(95% confidence interval/CI)：是一种用于估计未知参数的真实值范围的统计方法。它基于样本数据来估计某个未知参数（如平均值）的值，并给出一个区间（如(1.5, 4.7)），使得这个区间有95%的可能性包含这个未知参数的真实值

应用：理解效应大小的不确定性。如果CI包含了0，这通常意味着该效应在统计上是不显著的（与零假设相符），反之则通常意味着效应是统计显著的

相关系数(correlation coefficient)：用于描述两个变量之间的相关程度。一般在[-1, 1]之间，其绝对值越趋近于1，则两个变量相关程度越高。R中常用cor.test()函数计算该值

参数检验

基础概念与数据准备

参数检验(parametric tests)：

包括：t-test、analysis of variance方差分析、linear regression线性回归等
条件：数据有较明确的分布（如正态分布等），或假设数据有明确的分布（当假设不成立时，检测会无效）
特点：相比与非参数检验，更灵敏，p-value更低
适用于：数量化性状（如身高、体重、产量、污染值等）、整数值（如成绩、年龄、每天步数等）
不适用于：百分比或比例、有太多趋向于min/max的数据、count data（一种行为在固定时间内发生的次数）、discrete data（离散数据）
要求：
- 随机取样
- 值或残差(residules)为正态分布，残差是指观察值与预测值(mean)之差
- 有相同的方差

可能需要的包：psych、rcompanion、FSA、relaimpo

if(!require("psych", quietly = T))
{
  install.packages("psych");
  library("psych");
}
if(!require("rcompanion", quietly = T))
{
  install.packages("rcompanion");
  library("rcompanion");
}
if(!require("FSA", quietly = T))
{
  install.packages("FSA");
  library("FSA");
}
if(!require("relaimpo", quietly = T))
{
  install.packages("relaimpo");
  library("relaimpo");
}

准备数据：

source("data/input_data1.R");
str(Data);
headTail(Data);

'data.frame':	26 obs. of  5 variables:
 $ Student: chr  "a" "b" "c" "d" ...
 $ Sex    : chr  "female" "female" "female" "female" ...
 $ Teacher: chr  "Catbus" "Catbus" "Catbus" "Catbus" ...
 $ Steps  : int  8000 9000 10000 7000 6000 8000 7000 5000 9000 7000 ...
 $ Rating : int  7 10 9 5 4 8 6 5 10 8 ...

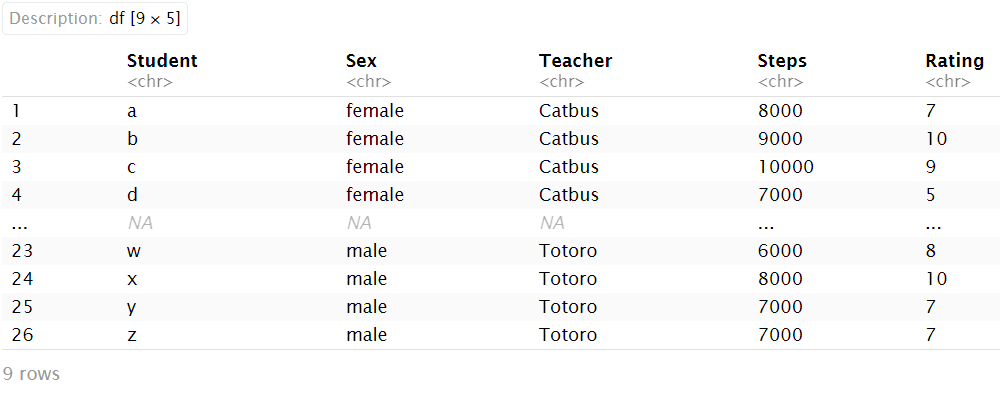
参数检验1

我们现在把该数据集按性别分成两组，探究步数Steps与性别Sex的关系

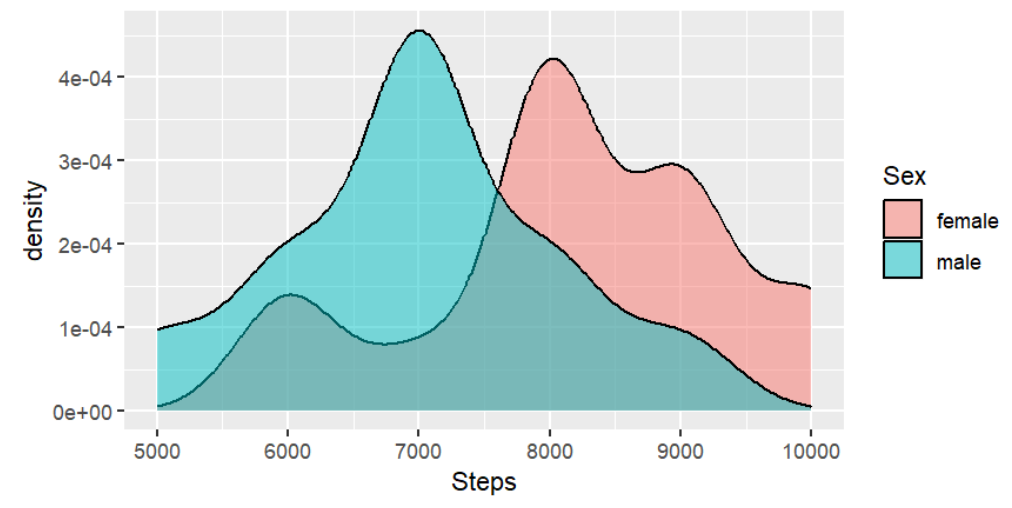
首先要看一看数据的分布：

ggplot(Data, aes(Steps, fill = Sex)) +  # 按sex列填充颜色并分组
       geom_density(position="dodge", alpha = 0.5);

参数检验2

M1 = mean(Data$Steps[Data$Sex=="female"])  # female的平均步数
M2 = mean(Data$Steps[Data$Sex=="male"])  # male的平均步数
Data$Mean[Data$Sex=="female"] = M1
Data$Mean[Data$Sex=="male"] = M2  # 添加到mean列
Data$Residual = Data$Steps - Data$Mean  # 计算残差
Data;
plot(jitter(Residual) ~ Mean, data = Data, las = 1);

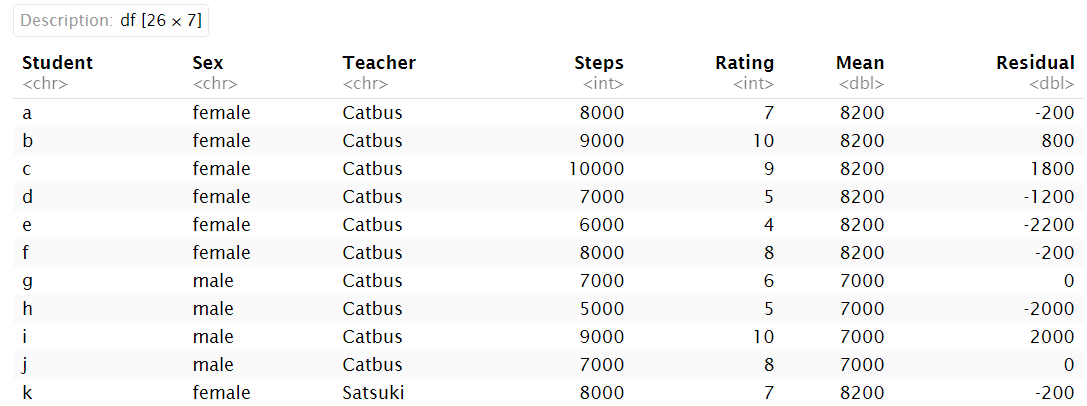
参数检验3

参数检验4

其中jitter函数对散点添加随机的“抖动”效果，将散点适当地沿x轴刻度两侧拓展，可以一定程度上避免常规散点图中点过于重叠的情况

异常值

异常值：指远远超出其他观测值的极端值

对于正态分布，通常是mean±3*sd或mean±2*sd范围外的值
对于非参数分布：

即1/4位点-IQR至3/4位点+IQR范围外的值

其中IQR=3/4位点-1/4位点，可使用同名函数IRQ()计算

用箱型图表示异常值：

s <- summary( swiss$Infant.Mortality );
iqr <- IQR(swiss$Infant.Mortality);
ggplot( swiss, aes( y =  Infant.Mortality ) ) + 
  geom_boxplot() +  # 画箱型图
  coord_flip() +  # 翻转坐标轴使箱型图横向
  geom_hline( 
    yintercept = c( s["1st Qu."] - 1.5 * iqr, s["3rd Qu."] + 1.5 * iqr ),  # 添加平行于y轴的直线，作为异常值的分界线
    colour = "red", linewidth = 2, linetype = 2
  );

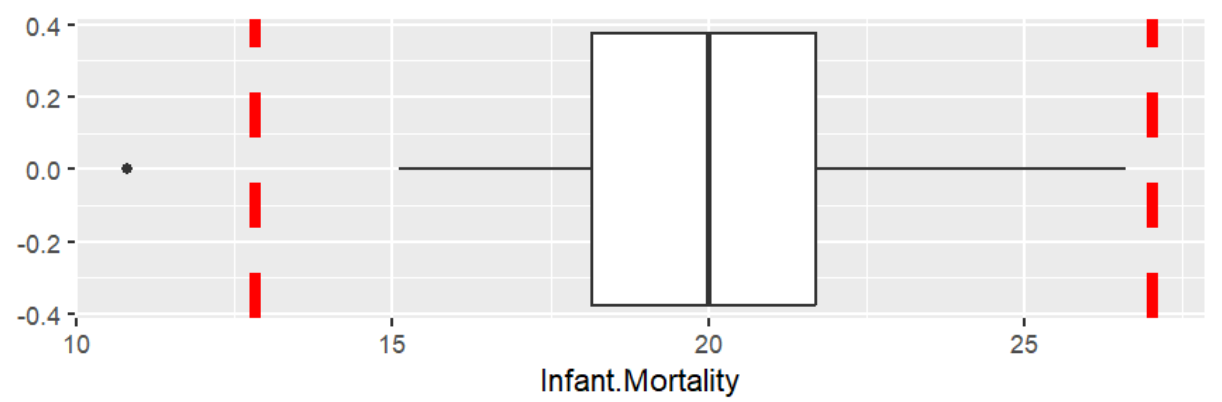
参数检验6

可以看到在左侧分界线的左面有一个异常值

t-test

参考文章1 参考文章2

使用t.test(x,y,...)函数

t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

参数检验7

在本例中，可以进行两种t-test：one sample t-test和two samples t-test

one sample t-test：检测分布是否与预期一致。比如男生每天的步数是否显著区别于1万

with( Data, t.test( Steps[ Sex == "male" ], mu = 10000 ) );

	One Sample t-test

data:  Steps[Sex == "male"]
t = -9.083, df = 10, p-value = 3.81e-06
alternative hypothesis: true mean is not equal to 10000
95 percent confidence interval:
 6264.07 7735.93
sample estimates:
mean of x 
     7000 

由结果可以看出，数据的均值为7000，p值<0.05，有区别

two samples t-test：按性别分成两组，探究步数Steps与性别Sex的关系

with( Data, t.test( Steps ~ Sex ) )
with( Data, t.test( Steps[ Sex == "male" ], Steps[ Sex == "female" ] ) )

这两种方法只是写法上有区别，结果相同

	Welch Two Sample t-test

data:  Steps by Sex
t = 2.6424, df = 22.816, p-value = 0.01461
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
  260.1421 2139.8579
sample estimates:
mean in group female   mean in group male 
                8200                 7000 

另一个例子：paired two sample t-test

# 准备数据
source("data/talk10/input_data2.R");
headTail(scores);

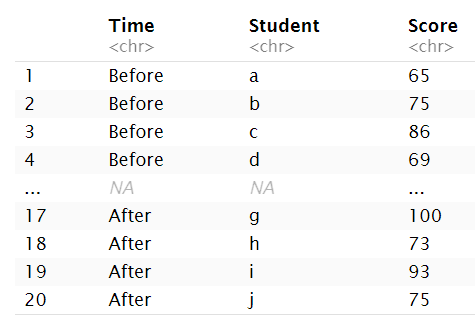
参数检验8

现要按time列分组，比较before和after两组的成绩score有无显著差别

很容易想到使用上面的方式：

scores$Score <- as.numeric(scores$Score);
with( scores, t.test( Score ~ Time ) );

	Welch Two Sample t-test

data:  Score by Time
t = 1.9742, df = 17.902, p-value = 0.064
alternative hypothesis: true difference in means between group After and group Before is not equal to 0
95 percent confidence interval:
 -0.6592429 21.0592429
sample estimates:
 mean in group After mean in group Before 
                82.7                 72.5 

观察结果可以看到p值>0.05，结果不显著

可能的原因：我们应该比较的是每个学生after和before的差别，而不是简单的分组取平均值

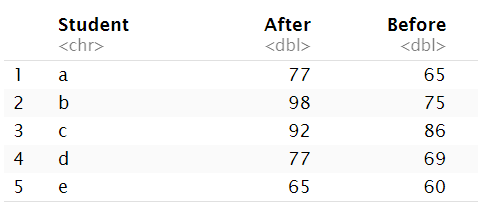
解决办法：将数据由长变宽，包含student、before、after列，列值表示每个学生after和before的成绩

scores.wide <- scores %>% 
  spread( Time, Score );  # 将time列的列值变列名，新列值来自score列
head(scores.wide, n = 5);
with( scores.wide, t.test( After, Before, paired = T ) );  # 注意指定参数paired = T标明是配对检验

参数检验9

	Paired t-test

data:  After and Before
t = 3.8084, df = 9, p-value = 0.004163
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
  4.141247 16.258753
sample estimates:
mean difference 
           10.2 

可以看到p值<0.05，before和after组有差别

ANOVA

参考文章

方差分析(analysis of variance/ANOVA)：可以检验三个或以上的样本均值是否存在显著差异，通常用于分析一个（或两个）变量对另一变量的贡献度/解释度/影响度

单因素ANOVA(One-Way ANOVA)：分析一个自变量在三个或更多水平上对因变量的影响，例如班级对学生的体重是否有影响

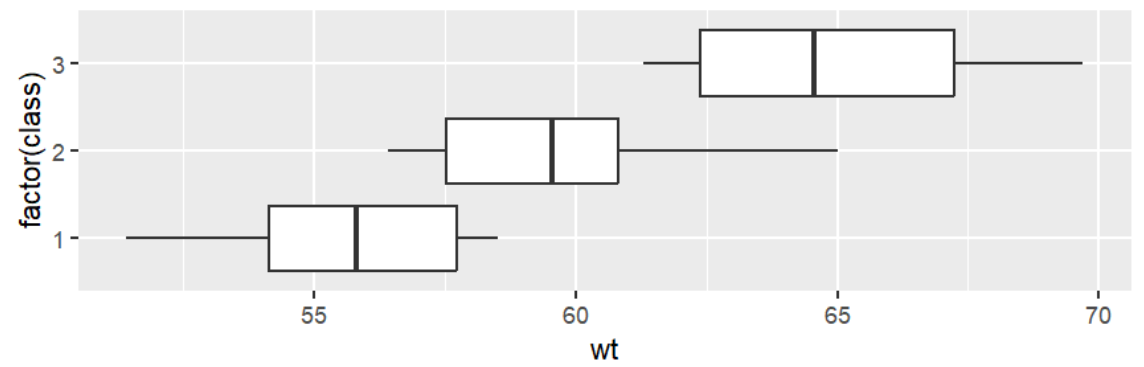
数据准备：三个班学生的体重

wts <- bind_rows( tibble( class = 1, wt = sample( seq(50, 60, by = 0.1), 20 ) ),
                  tibble( class = 2, wt = sample( seq(55, 65, by = 0.1), 20 ) ),
                  tibble( class = 3, wt = sample( seq(60, 70, by = 0.1), 20 ) ));
ggplot(wts, aes( factor( class ), wt ) ) + geom_boxplot() + coord_flip();

ANOVA1

model <- lm( wt ~ class, data = wts );  # 构建模型：wt与class列的关系
anova( model );  # 使用stats::anova分析模型

Analysis of Variance Table

Response: wt
          Df  Sum Sq Mean Sq F value    Pr(>F)    
class      1 1139.56 1139.56  133.98 < 2.2e-16 ***
Residuals 58  493.31    8.51                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

其中我们重点关注两个值：F valueF值和Pr(>F)P值

F值：用来衡量组间方差和组内方差比例的统计量。一个较大的F值通常意味着至少有一组的平均值与其他组存在显著差异

注意：“较大”这个概念取决于自由度和相应的P值
P值：标明得到的F值是否显著。如果P值小于0.05，则认为样本间有差异（某个自变量对因变量有影响）；而如果大于0.05，一般就忽略F值大小，直接认为没有影响

除此之外，Sum Sq（平方和）也可表示因素引起的变异量，该值越大则该因素的影响越大，与F值类似

在这个例子中，P值小于0.05，于是认为班级对学生的体重有影响

两因素ANOVA(Two-Way ANOVA)：分析两个自变量及其交互作用对因变量的影响，例如班级和年龄对体重的影响

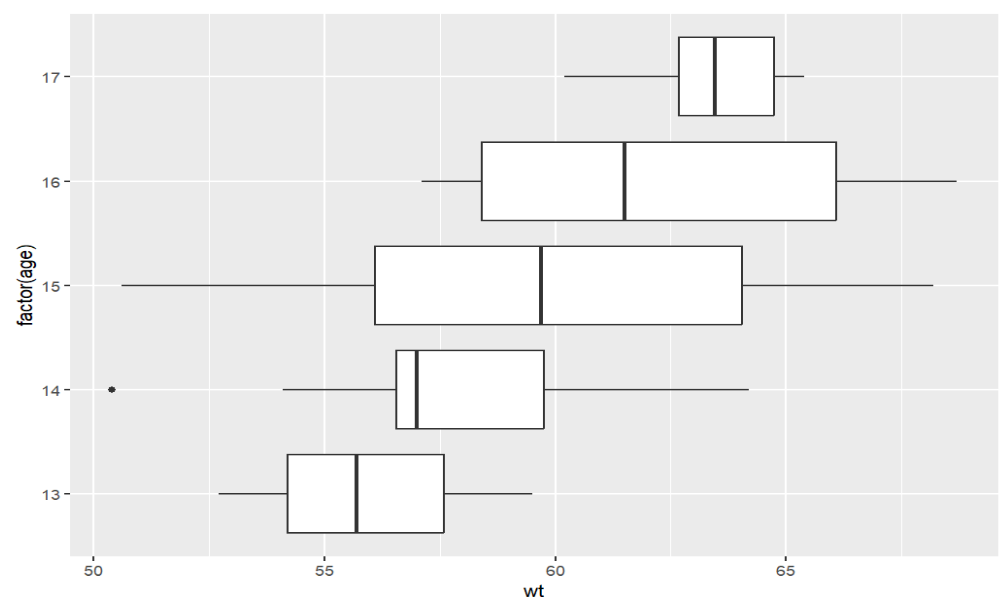
数据准备：三个班学生的体重和年龄

wts2 <- bind_rows( 
   tibble( class = 1, age = sample( 13:15, 20, replace = T ), wt = sample( seq(50, 60, by = 0.1), 20 ) ),
   tibble( class = 2, age = sample( 14:16, 20, replace = T ), wt = sample( seq(55, 65, by = 0.1), 20 ) ),
   tibble( class = 3, age = sample( 15:17, 20, replace = T ), wt = sample( seq(60, 70, by = 0.1), 20 ) )
);
ggplot(wts2, aes( factor( age ), wt ) ) + geom_boxplot() + coord_flip();  # 不同年龄对应的体重

ANOVA2

model3 <- lm( wt ~ class + age + class:age, data = wts2);
# 构建模型：wt与class列、age列以及class与age交互作用的关系
anova( model3 );

其中：class和age称为main effects，class:age称为interaction effects（交互作用）

Analysis of Variance Table

Response: wt
          Df Sum Sq Mean Sq F value    Pr(>F)    
class      1 770.88  770.88 89.6639 3.178e-13 ***
age        1   3.47    3.47  0.4035    0.5279    
class:age  1   1.50    1.50  0.1741    0.6781    
Residuals 56 481.46    8.60                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

可以看到只有class的p值小于0.05，所以只有班级才对体重有影响

更详细的查看每个因素对结果的影响：使用relaimpo包中的calc.relimp函数

res5 <- relaimpo::calc.relimp( wt ~ factor(class) + age + factor(class):age, data = wts2);
res5$R2;  # 总R2，即总影响
res5$lmg;  # 每个因素的贡献

[1] 0.6282798
factor(class) factor(class):age               age 
  0.527967912       0.001270408       0.099041446 

非参数检验

适用于总体的分布情况未知（或者不是正态分布），同时样本容量又小的情况

非参数检验对总体分布不做假设，直接从样本的分析入手推断总体的分布

非参数检验与参数检验的对比

注意：当正态性假设成立时，非参数检验通常不如相应的参数检验有力。因此如果数据是正态分布，仍应使用参数检验

wilcox test

用于检验两组数据是否存在显著差异

独立样本：wilcox.test(因变量 ~ 自变量)，例如两个班级的成绩是否有差异

非独立样本：wilcox.test(因变量 ~ 自变量, paired = TRUE)或wilcox.test(组1, 组2, paired = TRUE)，例如同一班级中每个学生在学期初和学期末的成绩是否有差异

source("data/input_data1.R");  # 装入数据：性别与步数的关系
with( Data, wilcox.test( Steps ~ Sex ) );

	Wilcoxon rank sum test with continuity correction

data:  Steps by Sex
W = 127.5, p-value = 0.01773
alternative hypothesis: true location shift is not equal to 0

p值<0.05，拒绝零假设（步数与性别没有关系），结论为”男性步数与女性步数有差别”（步数与性别有关系）

source("data/input_data2.R");
scores.wide <- scores %>% 
  spread( Time, Score );  # after和before两组成绩数据
with( scores.wide, wilcox.test( After, Before , paired=T) );

	Wilcoxon signed rank test with continuity correction

data:  After and Before
V = 53, p-value = 0.01078
alternative hypothesis: true location shift is not equal to 0

p值<0.05，after和before两组成绩数据有差异

更多例子

kruskal test

也是检验两组数据的差异，但与wilcox test统计学方法不同，常用于分析三个或更多的组和独立样本的检验

source("data/input_data1.R");  # 装入数据：性别与步数的关系
with( Data, kruskal.test( Steps ~ Sex ) );

	Kruskal-Wallis rank sum test

data:  Steps by Sex
Kruskal-Wallis chi-squared = 5.7494, df = 1, p-value = 0.01649

p值<0.05，男性步数与女性步数有差别

回归

主要参考文章

回归主要确定一个唯一的因变量(dependent variable)和一个或多个数值型的自变量(independent variable)之间的关系

之后根据这个关系对数据建立模型，来预测当自变量不同时因变量的结果

补充：因变量又称目标变量(target variable)/响应变量(response variable)，自变量又称预测变量(predictor variable)

线性回归

即使用直线进行回归分析的模型

Y可以被一个变量X解释：一元线性回归(simple linear regression/univariate linear regression)
Y可以被X、Z等多个变量解释：多元线性回归(multivariate linear regression)

线性回归的假设：

线性：X和Y的平均值之间的关系是线性的
同调性：残差的方差对于X的任何值都是相同的
独立性：观察是相互独立的
正态性：对于X的任何固定值，Y都是正态分布的

注意：

任何检验都有基本的假设
将检验应用于不符合假设的数据是统计学最大的滥用

lm

我们先以一元线性回归为例

lm函数是一种构建线性回归模型的方法：lm(因变量 ~ 自变量, data=数据集)

(m <- lm(Fertility ~ Education, data = swiss));

Call:
lm(formula = Fertility ~ Education, data = swiss)

Coefficients:
(Intercept)    Education  
    79.6101      -0.8624 

得到的结果m就是构建的线性回归模型，之后的分析都是对它的分析

返回的数据中，Coefficients是“系数”的意思，表示对应变量在直线方程中的系数

在此例中，得到的线性方程应为y=-0.8624x+79.6101，x指Education，y指Fertility

通常我们使用summary函数对模型进行详细分析

summary(m);

Call:
lm(formula = Fertility ~ Education, data = swiss)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.036  -6.711  -1.011   9.526  19.689 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  79.6101     2.1041  37.836  < 2e-16 ***
Education    -0.8624     0.1448  -5.954 3.66e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.446 on 45 degrees of freedom
Multiple R-squared:  0.4406,	Adjusted R-squared:  0.4282 
F-statistic: 35.45 on 1 and 45 DF,  p-value: 3.659e-07

参考文章

其中我们重点关注Coefficients部分，依次四个值是：

Estimate  Std.Error   t value   Pr(>|t|)
  估值     标准误差      T值        P值

当p值<0.05时，就可以认为对应的估值是较准确（显著）的，可以作为回归方程中的系数

之后的Multiple R-squared“拟合优度”和Adjusted R-squared“修正的拟合优度”，标明回归方程对样本的拟合程度怎么样，这个值越高（越趋近于1）越好，可以看到这里的修正拟合优度只有0.4282，说明拟合程度并不高

最后的F-statistic“F值”和p-value“F检验的p值”，用于判断方程整体的显著性，其p值<0.05，说明方程通过显著性检验

总结：

T检验（Coefficients部分）是检验解释变量的显著性的
R-squared是查看方程拟合程度的
F检验是检验方程整体显著性的

我们可以用coef函数获取模型得到的方程系数

coef( m ); 
coef( m )[1]; 
coef( m )["Education"]; 

(Intercept)   Education 
 79.6100585  -0.8623503 
(Intercept) 
   79.61006 
 Education 
-0.8623503 

除此之外，lm结果分析函数还有：

coefficients(m)模型系数（类似于coef）
confint(m, level=0.95)各个系数的95%置信区间
residuals(m)残差
anova(m)方差分析
vcov(m)协方差
influence(m)回归诊断

预测

使用predict(model, data)或者fitted(model, data)根据构造的线性模型model对数据集data进行预测，data作为模型中的自变量，返回使用模型计算后的因变量

注：data应包括model中所有的自变量列，如使用

df <- data.frame(x1=c(3, 4, 4, 5, 5, 6, 7, 8, 11, 12),
                 x2=c(6, 6, 7, 7, 8, 9, 11, 13, 14, 14),
                 y=c(22, 24, 24, 25, 25, 27, 29, 31, 32, 36))
model <- lm(y ~ x1 + x2, data=df)

创建的模型，就需要使用包含x1和x2列的data预测

new <- data.frame(x1=c(5),  # 注意列名必须为x1/x2，不能是其它值
                  x2=c(10))
predict(model, newdata = new)

实际应用：

m <- lm(Fertility ~ Education, data = swiss)
predictions <- m %>% predict( swiss );

在这段代码中，我们构建了swiss$Fertility~swiss$Education的模型，又将原数据swiss$Education作为自变量传入模型中，得到预测的因变量Fertility。

可以想到，预测结果predictions与原因变量swiss$Fertility越相似，模型越准确

还可以使用coef函数得到的系数手动计算预测结果：Fertility = a * Education + intercept

a <- coef( m )["Education"];
intercept <- coef( m )[1]
predictions2 <- a * swiss$Education + intercept;

得到的结果与上面predict函数相同

如何判断是否相似：

# 构建df，有两列，分别是预测值和真实值
predict_actual <- data.frame( PREDICITON = predictions, ACTUAL = swiss$Fertility );
# 画散点图，横纵坐标分别是预测和真实值
ggplot(predict_actual, aes( PREDICITON, ACTUAL )) + 
  geom_point() + 
  ggtitle("SWISS DATA 1888 Fertility") + 
  geom_abline(intercept = 0, slope = 1, colour = "red");  # 添加标准线y=x

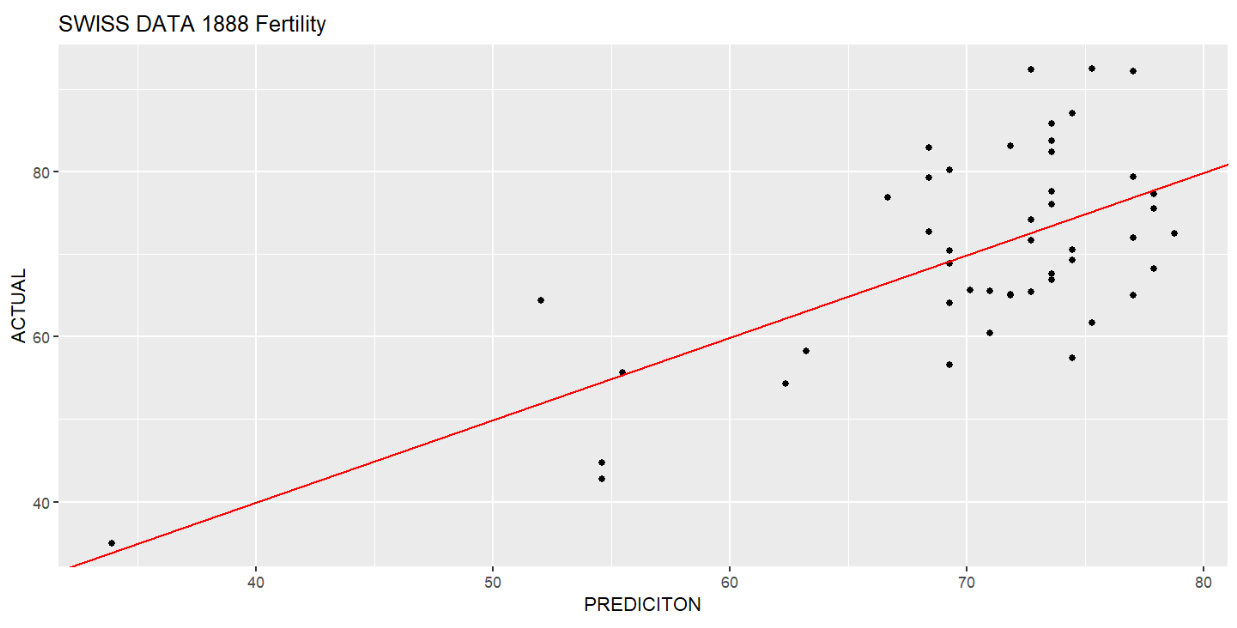
线性回归1

数据点(PREDICITON, ACTUAL)越靠近y=x，说明PREDICITON越相近于ACTUAL，预测越准确

上面是直观体现预测是否接近真实值的方法，也可以计算R方（拟合优度），除了summary函数中的summary(m)$r.squared，还可以：

cor.test函数：

cortest <- cor.test(swiss$Fertility,predictions)
cortest$estimate**2  # 0.4406156 

caret包：

if(!require("caret", quietly = T))
{
  install.packages("caret");
  library("caret");
}
data.frame(
  RMSE = RMSE(predictions, swiss$Fertility),
  R2 = R2(predictions, swiss$Fertility)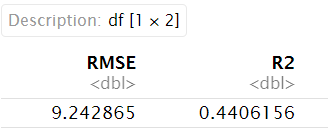
)

线性回归2

其中RMSE为均方根误差，越小模型越准确

interactions

即多元线性回归因素之间的依赖关系或互作关系，这里我们用datarium包中的marketing数据集作多元线性回归分析，展示各因素间的相互作用

if(!require("datarium", quietly = T))
{
  install.packages("datarium");
  library("datarium");
}
head(marketing);

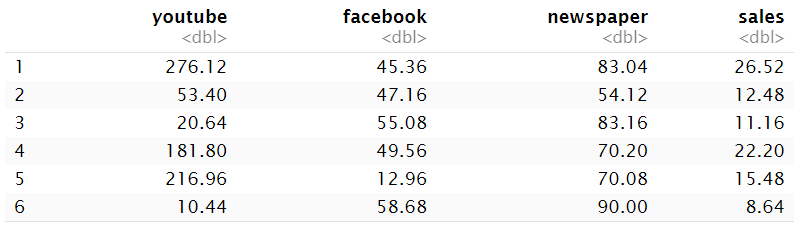
线性回归3

共有4列，其中3列是广告投放的地点(youtube/facebook/newspaper)，sales就是销量

我们要分析的就是不同广告投放地点对销量的影响，其中销量作因变量，三种投放地点作自变量

先做一个普通的多元线性回归

m1 <- lm( sales ~ youtube + facebook + newspaper, data = marketing );
summary(m1);

Call:
lm(formula = sales ~ youtube + facebook + newspaper, data = marketing)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.5932  -1.0690   0.2902   1.4272   3.3951 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.526667   0.374290   9.422   <2e-16 ***
youtube      0.045765   0.001395  32.809   <2e-16 ***
facebook     0.188530   0.008611  21.893   <2e-16 ***
newspaper   -0.001037   0.005871  -0.177     0.86    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.023 on 196 degrees of freedom
Multiple R-squared:  0.8972,	Adjusted R-squared:  0.8956 
F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16

可以看到youtube和facebook对销量的影响是显著的

# 进行预测
predicted.m1 <- m1 %>% 
  predict( marketing );
# 作真实值~预测值散点图
data.frame(p = predicted.m1, actual = marketing$sales ) %>% 
  ggplot( aes(x = p, y = actual) ) + 
  geom_point() + 
  geom_abline(intercept = 0, slope = 1, colour = "red");
# 评估预测效果
library(caret);
data.frame(
  RMSE = RMSE(predicted.m1, marketing$sales ),
  R2 = R2(predicted.m1, marketing$sales )
);

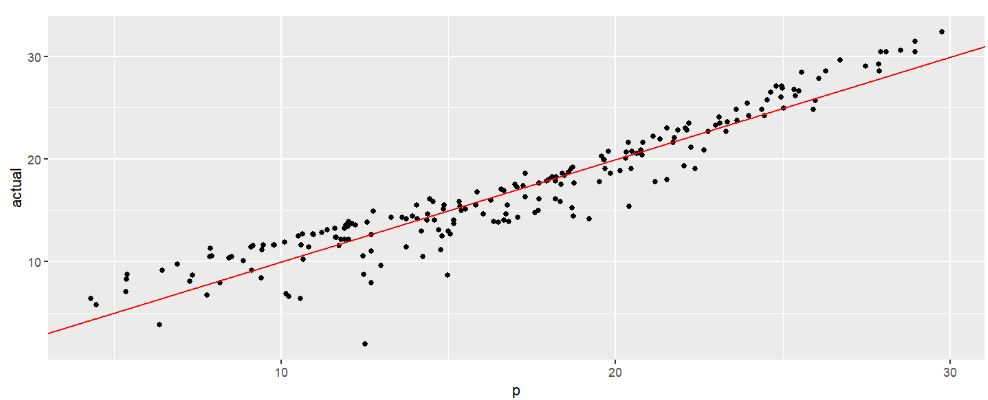
线性回归4

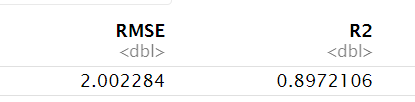
线性回归5

可以看出模型的预测效果还是可以的

相对重要性分析：各个自变量对因变量具体的影响程度

library(relaimpo);
calc.relimp( sales ~ youtube + facebook + newspaper, data = marketing );

重点关注结果中Relative importance metrics部分，它标明了每个因素的影响

Relative importance metrics: 

                 lmg
youtube   0.58527298
facebook  0.28878652
newspaper 0.02315114

可以看到youtube的影响最大，facebook其次，而newspaper影响很小

# 有newspaper的模型
m_with_newspaper <- lm(sales ~ youtube + facebook + newspaper, data = marketing);
# 没有newspaper的模型
m_without_newspaper <- lm(sales ~ youtube + facebook, data = marketing);
# 检验两个模型间的差异
anova(m_with_newspaper, m_without_newspaper);

Analysis of Variance Table

Model 1: sales ~ youtube + facebook + newspaper
Model 2: sales ~ youtube + facebook
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1    196 801.83                           
2    197 801.96 -1  -0.12775 0.0312 0.8599

可以看到差异不显著（p值>0.05），因此在下面的分析中，我们可以把newspaper这个因素去掉，使用没有newspaper的模型

interactions互作关系：例如，在一平台上投放广告会促进另一个平台上广告的效果，因为两个平台的用户可能是重叠的，当在两个平台都看到广告时，更可能购买产品

方法：因变量 ~ 自变量1 + 自变量2 + 自变量1:自变量2或因变量 ~ 自变量1 * 自变量2

m4 <- lm( sales ~ youtube + facebook, data = marketing );  # 没有interactions的模型
m5 <- lm( sales ~ youtube + facebook + youtube:facebook, data = marketing );  # 等效于↓
# m5 <- lm( sales ~ youtube*facebook, data = marketing );
anova(m4, m5);  # 两个模式是否有差异？
data.frame(
  no_interactions = summary(m4)$r.squared,
  with_interactions = summary(m5)$r.squared
);  # 两个模型的预测效果

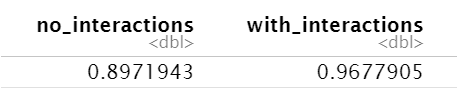
线性回归6 线性回归7

可以看到两个模型有显著差异（Pr(>F)<0.05），且加上互作分析后模型的预测效果更好

结论：在youtube和facebook两个平台同时投放广告最好

包含互作分析的相对重要性分析

library(relaimpo);
calc.relimp( sales ~ youtube*facebook, data = marketing );

Relative importance metrics: 

                        lmg
youtube          0.58851843
facebook         0.30867583
youtube:facebook 0.07059629

可视化的相互作用：检验facebook对youtube的影响

使用interactions包中的sim_slopes函数

if(!require("interactions", quietly = T))
{
  install.packages("interactions");
  library("interactions");
}
m6 <- lm( sales ~ youtube*facebook, data = marketing );
sim_slopes(m6, pred = youtube, modx = facebook, jnplot = TRUE)

线性回归9

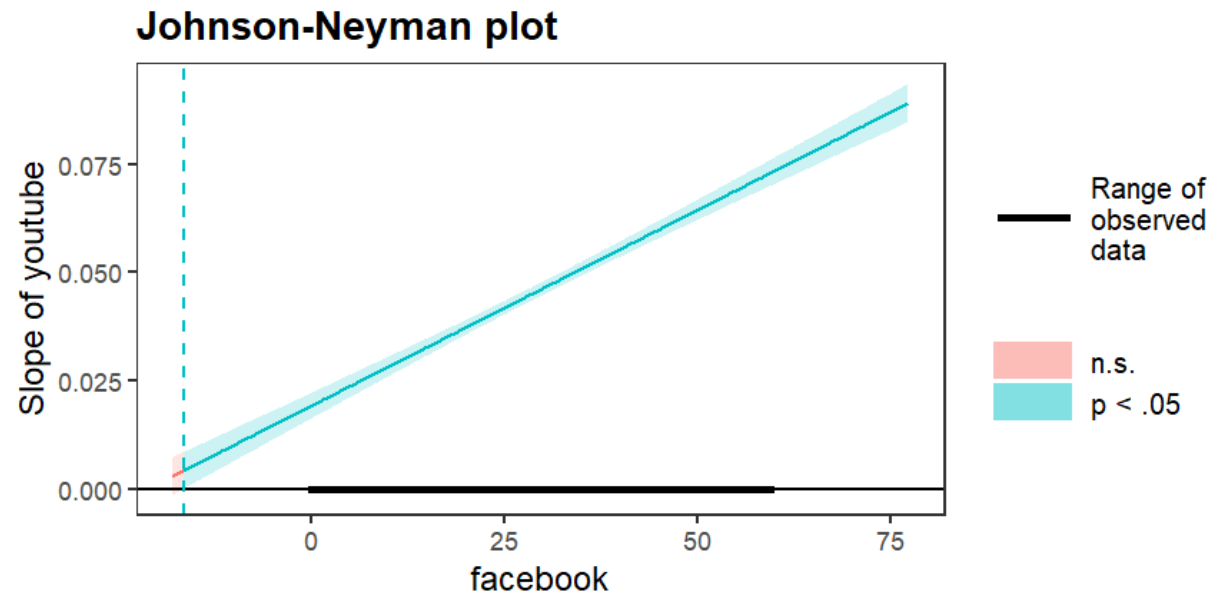
线性回归10

参考视频

sim_slopes中m6是预测模型，pred是自变量(facebook)，modx是因变量(youtube)

图中

蓝色部分的区域：当自变量在该区域时，对因变量的影响显著；红色则代表不显著

红色区域对应文字结果中[-26.70, -16.41]部分
```
When facebook is OUTSIDE the interval [-26.70, -16.41], 
the slope of youtube is p < .0
```
直线表示因变量~自变量模型的斜率，即直线在x轴以上(>0)时，表示自变量对因变量有正向影响；反之是负向影响
直线两侧的两条曲线就是置信区间，当置信区间不包括0点时，影响显著

一个其它的johnson-neyman plot可以更好的说明这一点：

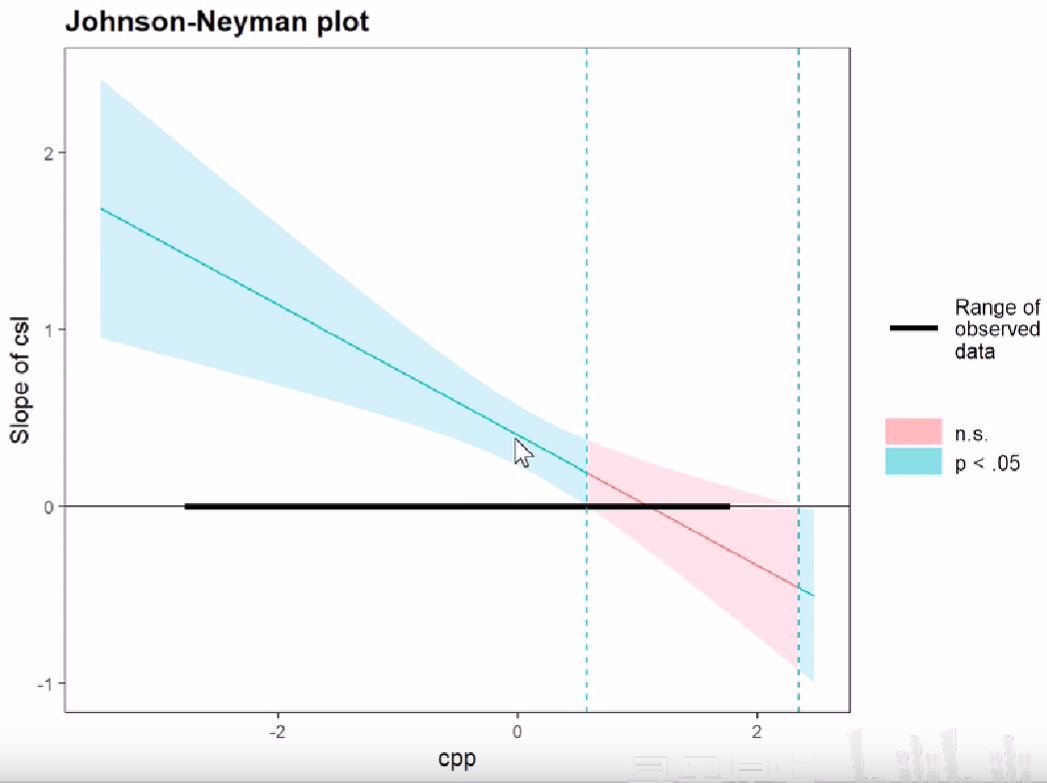
可以看到当置信区间的两条线的中间区域不跨过x轴时，是蓝色，反之是红色
x轴上画粗的部分就是自变量实际的取值范围

对应文字结果中[0.00, 59.52]部分
```
Note: The range of observed values of facebook is [0.00, 59.52]
```

glm

即广义线性模型

用法类似于lm，不同的是它可以使用family参数指定数据的分布，并分析非正态分布的数据

当family=gaussian即数据正态分布（高斯分布）时，它与lm()完全相同

m.lm <- lm(am ~ disp + hp, data=mtcars);
m.glm <- glm(am ~ disp + hp, data=mtcars);
coef(m.lm);
coef(m.glm);

 (Intercept)         disp           hp 
 0.755928587 -0.004289191  0.004362551 
 (Intercept)         disp           hp 
 0.755928587 -0.004289191  0.004362551 

使用glm拟合二项分布模型

二项分布模型：因变量Y只有两个值，比如1/0

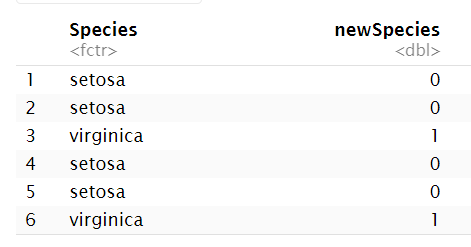
# 选出iris中Species列为"setosa"和"virginica"的行
dat <- iris %>% 
  dplyr::filter( Species %in% c("setosa", "virginica") );
dat$newSpecies <- ifelse(  # 将字符串列值转成数值型
  dat$Species == "setosa", 0, 1
);  # "setosa"->0  "virginica"->1
head(dat %>% sample_n(6) %>% dplyr::select(Species, newSpecies));  # 随机选出6行展示

线性回归11

# 构建模型：Sepal.Length对Species即newSpecies的影响
bm <- glm( 
  newSpecies ~ Sepal.Length, 
  data = dat,  # 数据集
  family = binomial  # 二项分布
);
bm;
summary(bm);

Call:  glm(formula = newSpecies ~ Sepal.Length, family = binomial, data = dat)

Coefficients:
 (Intercept)  Sepal.Length  
     -38.547         6.805  

Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
Null Deviance:	    138.6 
Residual Deviance: 26.25 	AIC: 30.25

Call:
glm(formula = newSpecies ~ Sepal.Length, family = binomial, data = dat)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -38.547      9.557  -4.033 5.50e-05 ***
Sepal.Length    6.805      1.694   4.016 5.91e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

重点关注两个值：

bm中的AIC：赤池信息准则(Akaike Information Criterion)，值越小拟合效果越好
summary(bm)中的Pr(>|z|)：<0.05则说明Sepal.Length对Species影响显著

可以看到Sepal.Length增大使newSpecies增大，越趋近于”virginica”

# 使用模型进行预测
data.frame( 
  predicted = bm %>% predict( dat ),
  original = dat$Species 
) %>% 
  sample_n(10);

线性回归12

可以看到，predict越小，则代表Species越可能是”setosa”

使用type="response"进行预测

在predict函数中设置type="response"参数，得到的是预测概率，即预测结果为1的概率

data.frame( 
  predicted_response = bm %>% predict( dat, type = "response" ),  
  original = dat$Species 
) %>% 
  sample_n(5);

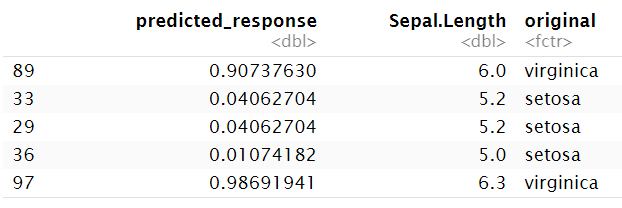
线性回归13

这5行分别表示：

根据Sepal.Length=6.0预测newSpecies有0.907的概率为1（即有很大概率Species为”virginica”）
根据Sepal.Length=5.2预测newSpecies有0.041的概率为1（即有很大概率Species为”setosa”）
根据Sepal.Length=5.2预测newSpecies有0.041的概率为1（即有很大概率Species为”setosa”）
根据Sepal.Length=5.0预测newSpecies有0.011的概率为1（即有很大概率Species为”setosa”）
根据Sepal.Length=6.3预测newSpecies有0.987的概率为1（即有很大概率Species为”virginica”）

除此之外，glm还可用于泊松分布的预测，设置family=poisson

原理相同，这里不作介绍

非线性回归

非线性回归(Non-linear regression/nls)：使用由一个或多个自变量组成的非线性函数来预测目标变量

nls(因变量~包括自变量的公式, start=list(参数1=初始值, ...))

例：

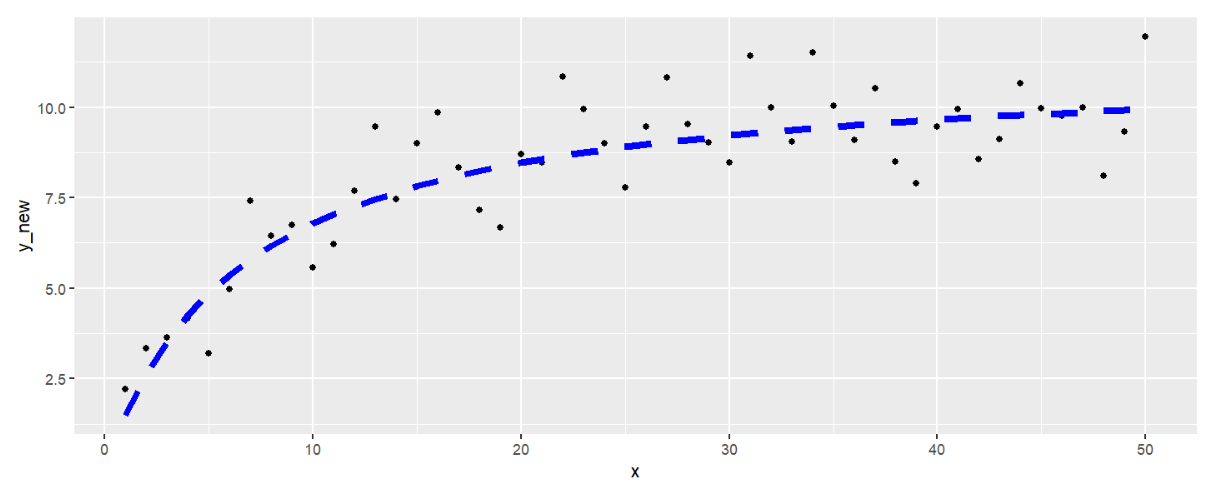
# 准备数据
x <- c(1:50);  # 1,2,...,50
a <- runif(1, 10, 20);  # 生成一个10-20间的数
b <- runif(1, 0, 10);  # 生成一个0-10间的数
y <- (a*x)/(b+x);  # y=a*x/(b+x)
y_new <- y+rnorm(50,0,1);  # 为数据添加随机的抖动
ggplot() +  # 展示数据
  geom_point(aes(x=x, y=y_new)) +  # 散点图
  geom_line(aes(x=x, y=y),lty=2,col="blue",lwd=2);  # y~x关系

非线性回归1

# 进行预测
m <- nls(
  y_new ~ pre_a*x/(pre_b+x),  # 指定y与x间的关系为y=a*x/(b+x)
  start = list(pre_a=0.1, pre_b=0.1)  # 指定a与b的起始值（从这个值开始尝试拟合）
);  # 
print(paste0('true a:', a));
print(paste0('true b:', b));
summary(m);

[1] "true a:11.2422794732265"
[1] "true b:6.57833542907611"

Formula: y_new ~ pre_a * x/(pre_b + x)

Parameters:
      Estimate Std. Error t value Pr(>|t|)    
pre_a   11.284      0.444  25.415  < 2e-16 ***
pre_b    6.113      1.072   5.701 7.15e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.097 on 48 degrees of freedom

Number of iterations to convergence: 9 
Achieved convergence tolerance: 2.399e-06

可以看到两个参数的p值都<0.05，且与实际值很接近

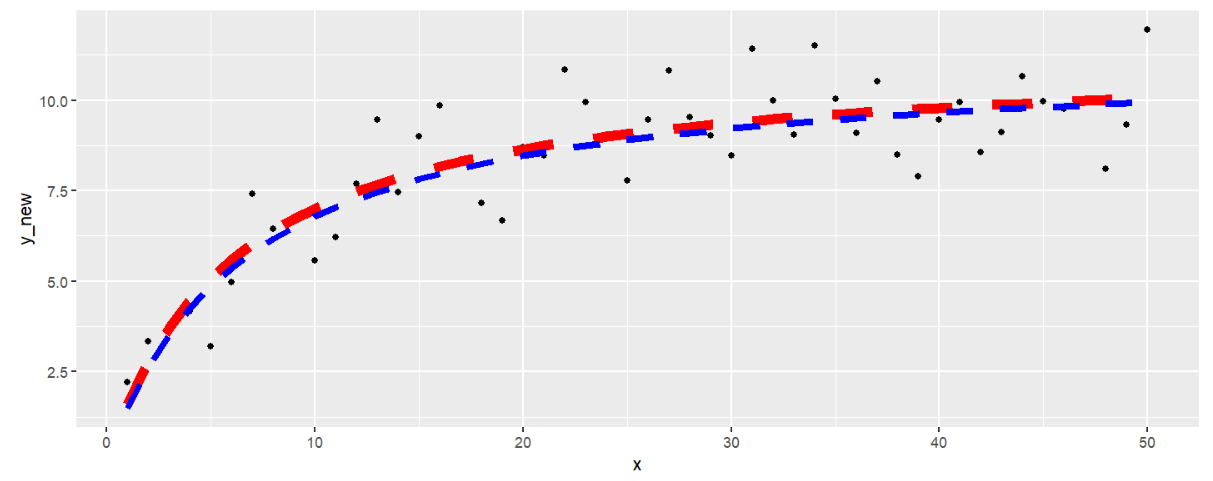
# 看看预测出来的曲线
ggplot() +
  geom_point(aes(x=x, y=y_new)) +
  geom_line(aes(x=x, y=predict(m, x)),lty=2,col="red",lwd=3) +  # 预测曲线
  geom_line(aes(x=x, y=y),lty=2,col="blue",lwd=2);  # 实际曲线

非线性回归2

也可使用drc包：

if(!require("drc", quietly = T))
{
  install.packages("drc");
  install.packages('carData');
  library("drc");
}

它的拟合函数可以提供公式模板，不需指定包含自变量的公式，以及各参数初始值

# 使用上例的数据生成方法
x <- seq(0,50,1);
y_old <- (runif(1,10,20)*x)/(runif(1,0,10)+x);
y <- y_old+rnorm(51,0,1);
m_drc <- drm( y ~ x, fct = LL.3() );  # 使用LL.3()模型
ggplot() +
  geom_point(aes(x=x,y=y)) + 
  geom_line(aes(x=x, y=predict(m_drc)), col="red", linetype=2, ,lwd=3) +
  geom_line(aes(x=x, y=y_old),lty=2,col="blue",lwd=2);

非线性回归3

drm包配合aomisc包使用，后者提供了更多的模板，用于拟合更多的函数

if(!require("aomisc", quietly = T))
{
  if(!require("devtools", quietly = T))
  {
    install.packages("devtools");
    library("devtools");
  }
  devtools::install_github("onofriAndreaPG/aomisc");
  library("aomisc");
}

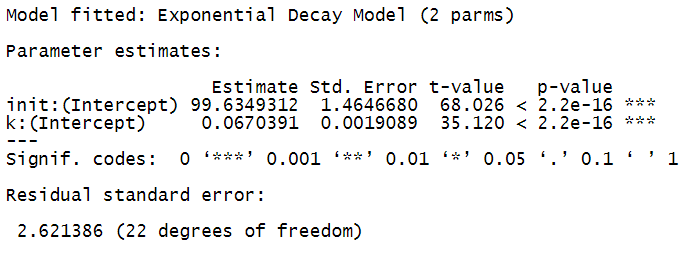
例1：Exponential decay指数衰减函数y = a * (exp(k * X) * k)

data(degradation);  # 载入数据degradation
m14 <- drm(
  Conc ~ Time, 
  data = degradation,
  fct = DRC.expoDecay()  # 指定模型
);
summary(m14);
plot(m14, log="");

非线性回归4

非线性回归5

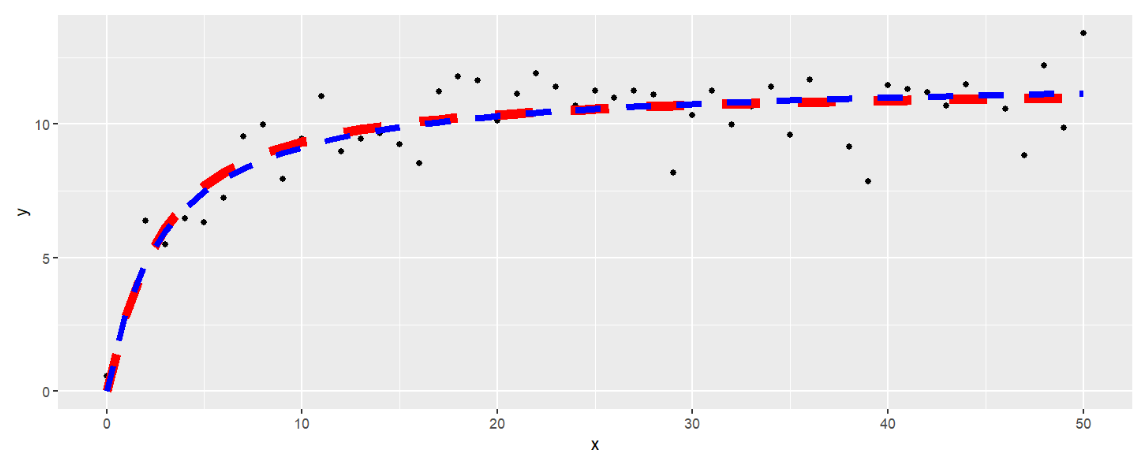
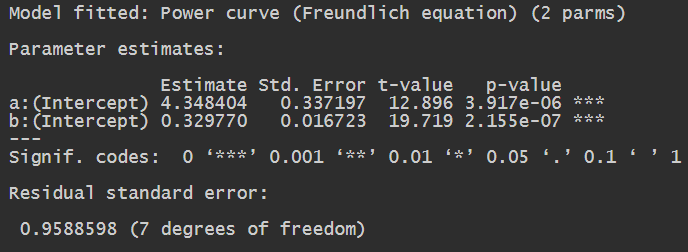
例2：Power curve功率曲线a * (X^(b - 1) * b)

data(speciesArea);  # speciesArea
m15 <- drm(
  numSpecies ~ Area, 
  data = speciesArea,
  fct = DRC.powerCurve()
);
summary(m15);
ggplot( speciesArea, aes(x= Area, y= numSpecies) ) +
  geom_point( aes(x= Area, y= numSpecies) ) + 
  geom_line( 
    aes(x = Area, y = predict( m15, speciesArea )), 
    colour = "red", linetype = 2 
  );

非线性回归6

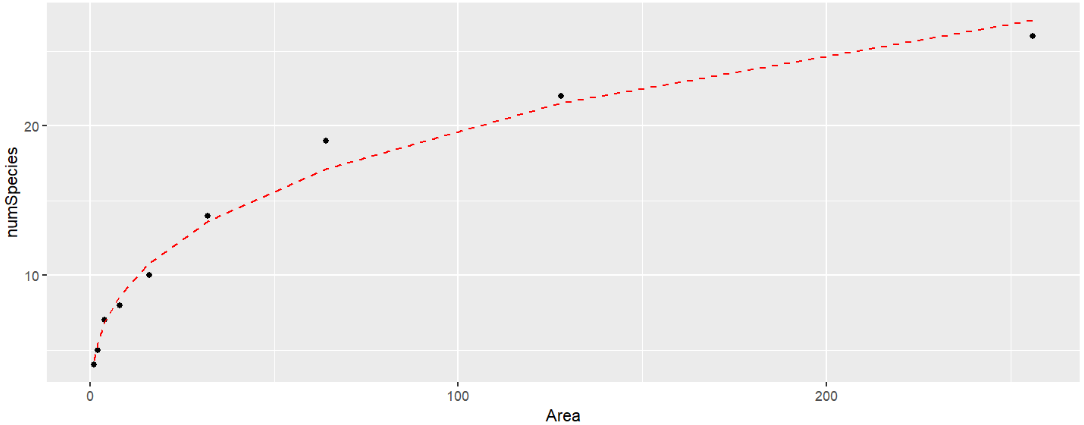
非线性回归7

与线性回归模型进行比较：

library(caret);
# 非线性回归模型
R2(  speciesArea$numSpecies, predict( m15, speciesArea ) );
# 线性回归模型
m16 <- lm( numSpecies ~ Area, data = speciesArea );
R2(  speciesArea$numSpecies, predict( m16, speciesArea ) );

[1] 0.9874392
[1] 0.8110041

可以看到非线性回归模型的R方更大，准确性更高

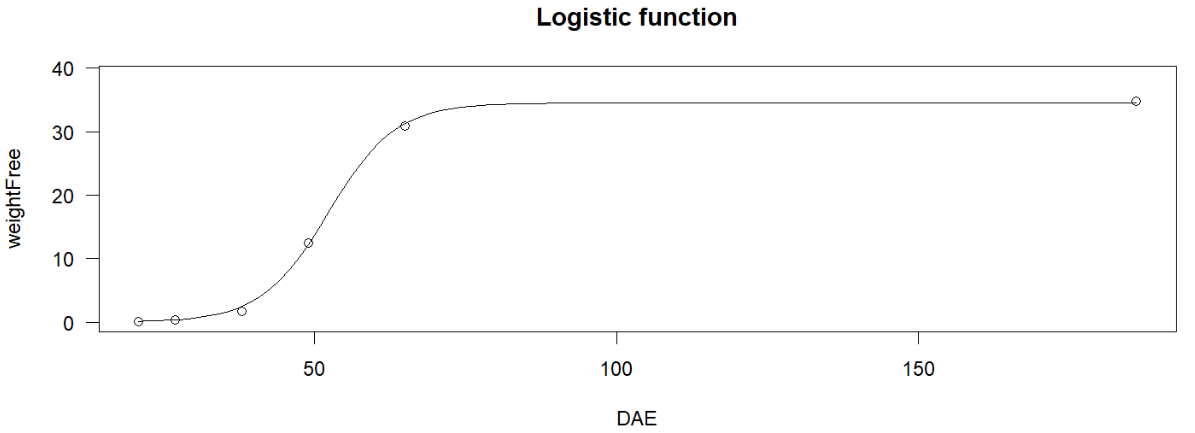
例3：logistic函数(logistic function)/S型曲线(sigmoid曲线)

data(beetGrowth);
m17 <- drm(
  weightFree ~ DAE, 
  data = beetGrowth,
  fct = L.3()
);
plot(m17, log="", main = "Logistic function");

非线性回归9

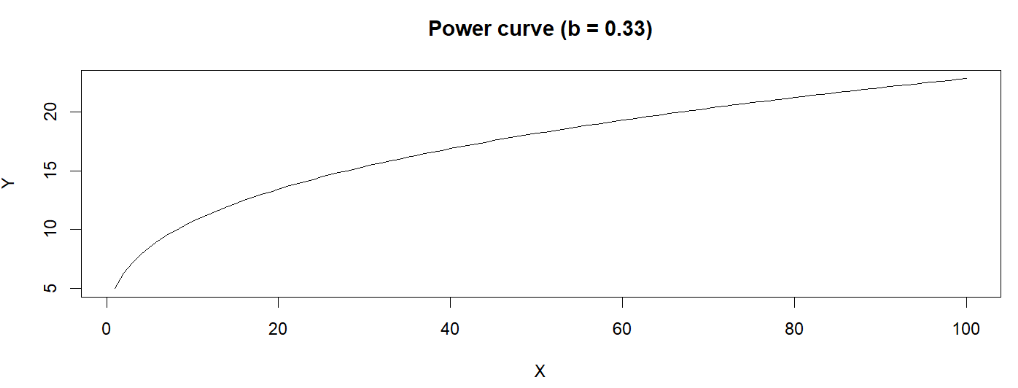
除此之外，drm包和aomisc包还可用于数据生成

如powerCurve.fun(x, a, b)可生成y = a * (X^(b - 1) * b)

plot(
  powerCurve.fun(1:100, 5, 0.33),
  xlab = "X", ylab = "Y",
  main = "Power curve (b = 0.33)", 
  type = "l"  # 将数据点隐藏
);

非线性回归8

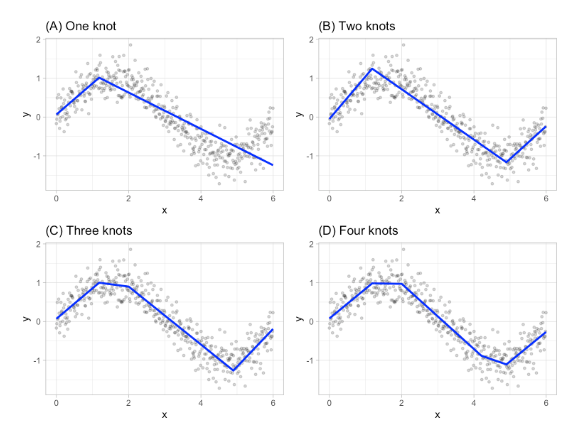
多元非线性回归简介

主要有两个方向：

MARS(Multivariate Adaptive Regression Splines)多元自适应回归样条
machine learning机器学习

这里以MARS为例

MARS提供了一种通过评估切割点(cutpoints)/节点(knots)来捕捉数据中非线性关系的便捷方法。该程序将每个预测器的每个数据点评估为一个节点，并使用候选特征创建线性回归模型

非线性回归10

一个例子：

# 准备数据
library(AmesHousing);  # The Ames Iowa Housing Data
ames <- AmesHousing::make_ames();
head(ames);

非线性回归11

# 进行拟合
library(earth);
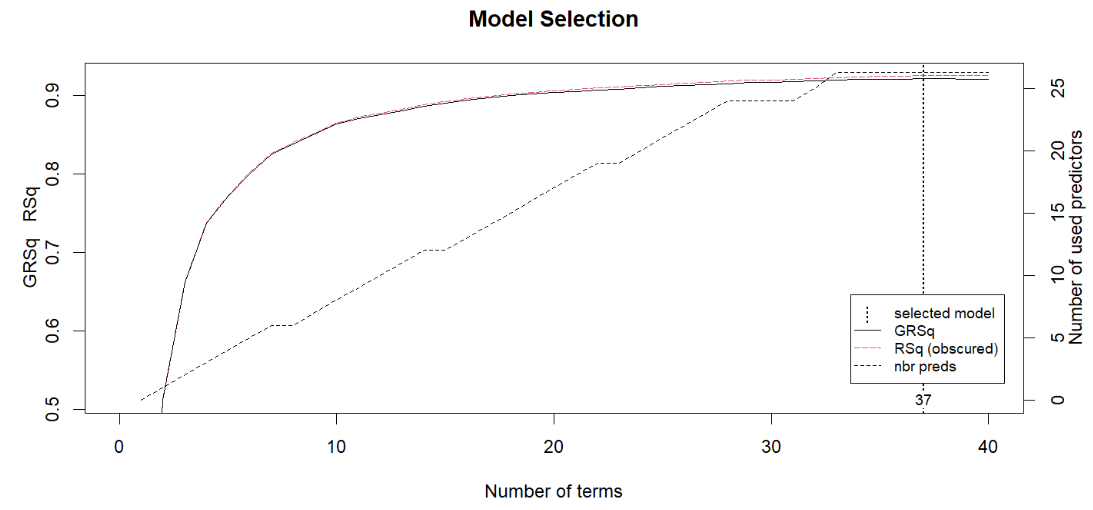
mars1 <- earth( Sale_Price ~ .,  data = ames );
print(mars1);
plot(mars1, which = 1);

非线性回归12

非线性回归13