数据分析01--NumPy

python-database

NumPy基础，包括ndarray数组、矩阵操作、文件操作等

import numpy as np

numpy基础

数据类型

数组中常见的数据类型：

int–int8 uint8 int16 int32 int64
float–float16 float32 float64
str字符串

如果需要将数据类型传入函数，就使用np.int8这种形式表示

ndarray数组

创建

列表直接创建

np.array(列表)

lst = [1,2,3,4,5]
nd = np.array(lst)
print(nd) #[1 2 3 4 5]
print(type(nd)) #<class 'numpy.ndarray'>

注意：因为numpy默认ndarray中所有元素类型相同，如果传入的列表中有不同类型，则会自动转换为同一类型，优先级str>float>int

print(np.array([3.1,2,"string"])) #['3.1' '2' 'string']
print(np.array([3.1,3])) #[3.1 3. ]

使用np函数创建

np.ones(shape,dtype=None,order='C')创建一个所有元素都为1的多维数组。

shape=(m,[n,...])控制创建m行n列的多维数组；dtype接收数据类型（可以是numpy的，也可以是python自带的int等）；order控制内存存储方式。一般只给第一个参数即可
```
n = np.ones(shape=(3,)) #创建有3个元素的一维数组
print(n) #[1. 1. 1.] 默认使用浮点数
n = np.ones(shape=(3,4),dtype=np.int8) #创建3行4列的二维数组，指定int类型
print(n) #[[1 1 1 1],[1 1 1 1],[1 1 1 1]]
#还可以有更高维，如shape=(3,4,5)
```
np.zeros(shape,dtype=None,order='C')创建一个所有元素都为0的多维数组。使用方式同上
np.full(shape,fill_value,dtype=None,order='C')创建一个所有元素都为fill_value的多维数组。使用方式同上
np.eye(row,col,k=0,dtype=None,order='C')创建row行col列的、主对角线（左上-右下）位置为1 其它位置为0的二维数组。其中col默认=row；k指定向右偏移k个位置，若为负数就是向左偏移

np.eye(3,3,dtype=np.int8)
```
[[1 0 0]
[0 1 0]
[0 0 1]]
```
np.eye(3,5,k=2,dtype=np.int8)
```
[[0 0 1 0 0]
[0 0 0 1 0]
[0 0 0 0 1]]
```

np.linspace(start,stop,num=50,endpoint=True,retstep=False,dtype=None)创建从start到stop的等差数列，该数列有num个数，步长根据这3个值自动进行计算；endpoint控制该数列是否包含结束值stop；retstep决定是否返回步长

n = np.linspace(0,10,num=6,dtype=np.int16) #默认包含结束值
print(n) #[ 0  2  4  6  8  10]
n = np.linspace(0,10,num=5,dtype=np.int16,endpoint=False,retstep=True) #设置不包含结束值
print(n) #(array([0, 2, 4, 6, 8], dtype=int16), 2.0) 可以看到结果中包含步长

np.arrange(start=0,stop,step=1,dtype=None)创建[start,stop)的步长为step的数组，类似于python中的range()。注意它不包含结束值
```
n1 = np.arange(10) #[0 1 2 3 4 5 6 7 8 9]
n2 = np.arange(2,10) #[2 3 4 5 6 7 8 9]
n3 = np.arange(2,10,2) #[2 4 6 8]
```
重点：np.random.randint(low,high=None,size=None,dtype=None)创建一个包含随机整数的多维数组：
- 当high=None时，生成数范围为[0,low)，如果给定high值，就生成[low,high)的数；
- size指定数组维数：size=6生成包含6个元素的一维数组，size=(3,4)生成3行4列的二维数组，更高维数也使用(x,y,z,...)形式创建
```
n1 = np.random.randint(10) #生成1个[0,10)的随机整数
n2 = np.random.randint(-10,11) #生成1个[-10,11)的随机整数
n3 = np.random.randint(3,size=5) #生成5个[0,3)的随机整数
n4 = np.random.randint(-2,high=3,size=(2,2)) #生成2*2的二维数组，元素取值为[-2,3)
```

np.random.randn(d0,d1,...,dn)创建一个服从标准正态分布的多维数组

n1 = np.random.randn() #产生一个随机数，该数服从标准正态分布
n2 = np.random.randn(10) #产生含有10个元素的一维数组，元素服从标准正态分布
n3 = np.random.randn(3,4) #产生3行4列的二维数组，元素服从标准正态分布

np.random.normal(loc=0,scale=1,size=None)创建一个服从正态分布的多维数组，可以指定均值和标准差
- loc指定均值，即正态分布的中心
- scale指定标准差，对应分布的宽度，该值越大则曲线越矮胖
- size指定数组维数，同randint函数（size=6生成包含6个元素的一维数组，size=(3,4)生成3行4列的二维数组，更高维数也使用(x,y,z,...)形式创建）
```
n1 = np.random.normal(loc=100,scale=10) #产生一个随机数，该数服从正态分布，均值为100，标准差为10
n2 = np.random.normal(loc=100,size=10) #产生含有10个元素的一维数组，元素服从正态分布，均值为100，标准差为1
```
np.random.random(size=None)创建一个元素为[0,1)的随机数的多维数组
- size指定数组维数，同randint函数（size=6生成包含6个元素的一维数组，size=(3,4)生成3行4列的二维数组，更高维数也使用(x,y,z,...)形式创建）
```
n1 = np.random.random() #产生一个[0,1)随机数
n2 = np.random.random(size=10) #产生含有10个元素的一维数组，元素取值为[0,1)
```

np.random.rand(d0,d1,...,dn)创建一个元素为[0,1)的随机数的多维数组，与random类似，参数使用同randn

n1 = np.random.rand() #产生一个随机数，该数取值为[0,1)
n2 = np.random.rand(10) #产生含有10个元素的一维数组，元素，该数取值为[0,1)
n3 = np.random.rand(3,4) #产生3行4列的二维数组，元素，该数取值为[0,1)

常用属性

ndim维度
shape形状–各维度的长度
size总长度
dtype元素类型

n = np.random.rand(3,4)
print(n.ndim) #2 表示2维数组
print(n.shape) #(3, 4) 表示3行4列（第一个维度长度为3，第二个为4）
print(n.size) #3*4=12 各维度长度相乘
print(n.dtype) #float64

常用操作

索引

一维时与列表相同：

n = np.array([0,1,2,3,4,5])
print(n[0]) #第一个元素0
print(n[-1]) #最后一个元素5

多维时类似列表：

n = np.array([[1,2,3],[4,5,6]])
print(n[0]) #第一行[1 2 3]
print(n[0][1]) #第一行第二个数2
print(n[0,1]) #是n[0][1]简写，也可以接收负数表示倒数第x行

就多了一个简写方式[1][2][-3]->[1,2,-3]

使用索引也可以直接对ndarray中的数据进行修改，如：

n = np.array([[1,2,3],[4,5,6]])
n[0] = [10,20,30] #修改第一行为[10,20,30]
n[1] = 100 #修改第二行为[100,100,100]
print(n) #[[ 10  20  30] [100 100 100]]

切片

与列表的切片相同，都可使用[start:end:step]的方式，因为一维ndarray切片与列表切片完全相同，以下展示二维的切片方法。

取行：
- 取一行–n[行索引]
- 取连续多行–n[开始行索引:结束行索引]注意是左闭右开区间
- 取不连续的多行–n[[行索引1,行索引2,...]]，其中行索引可以重复，注意有两层中括号
若取的是多行就返回一个新的二维数组，单行就返回一维数组
```
n = np.array([[11,12,13],[21,22,23],[31,32,33],[41,42,43],[51,52,53]])
n1 = n[0] #取第一行 [11 12 13]
n2 = n[1:3] #第2-3行 [[21 22 23] [31 32 33]]
n3 = n[[1,4,2,2]] #第2 5 3 3行 [[21 22 23] [51 52 53] [31 32 33] [31 32 33]]
```

取列：

取一列–n[:,列索引]表示取指定列的所有行
取连续的多列–n[:,开始列索引:结束列索引]
取不连续的多列–n[:,[列索引1,列索引2,...]]

若取的是多列就返回一个新的二维数组，单列就返回一维数组

n = np.array([[11,12,13],[21,22,23],[31,32,33],[41,42,43],[51,52,53]])
n1 = n[:,0] #取第一列 [11 21 31 41 51]
n2 = n[:,0:2] #第1-2列 [[11 12] [21 22] [31 32] [41 42] [51 52]]
n3 = n[:,[1,0,0]] #第2 1 1列 [[12 11 11] [22 21 21] [32 31 31] [42 41 41] [52 51 51]]

取行列：就是把上面两个合起来，中间用,隔开

n = np.array([[11,12,13],[21,22,23],[31,32,33],[41,42,43],[51,52,53]])
n1 = n[1:3,0] #取第2-3行的第一列 [21 31]
n2 = n[1,0:2] #第2行第1-2列 [21 22]
n3 = n[[1,3],[0,2]] #第2 4行的第1 3列 [21 43]

注意最后一行代码的实际意思是取第2行第一列+第4行第3列，而不是取第2行第1 3列+第4行第1 3列

应用：翻转

n = np.array([[11,12,13],[21,22,23],[31,32,33],[41,42,43],[51,52,53]])

[[11 12 13]
 [21 22 23]
 [31 32 33]
 [41 42 43]
 [51 52 53]]

行翻转：n1 = n[::-1]

[[51 52 53]
 [41 42 43]
 [31 32 33]
 [21 22 23]
 [11 12 13]]

列翻转：n2 = n[:,::-1]

[[13 12 11]
 [23 22 21]
 [33 32 31]
 [43 42 41]
 [53 52 51]]

例：对一张图片进行翻转

import numpy as np
import matplotlib.pyplot as plt
pic = plt.imread('active.png')
print(pic.shape) #(32, 102, 4) pic是一个三维数组，前两个维度分别是宽度，第三个维度是颜色
pic = pic[::-1] #上下翻转
pic = pic[:,::-1] #左右翻转
pic = pic[:,:,::-1] #翻转第三个维度（无实际意义），将会改变图片整体的配色
pic = pic[::10,::10] #隔10像素取一个值，对图片作模糊处理
plt.imshow(pic) #显示图片

增加

numpy.append(arr, values, axis=None)
- 不指定轴向时，将数组a，b都展平后进行追加
```
array([[1, 2, 3],
  [4, 5, 6]])
array([[7, 8, 9]])
```
```
np.append(a, values=b)
```
```
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9]) 
```
- 指定轴向时，根据轴向追加，且形状必须匹配（指定轴向为行追加时列数必须相等，指定轴向为列追加时行数必须相等）
```
np.append(a, values=b, axis=0) #根据行追加
```
```
array([[ 1,  2,  3],
 [ 4,  5,  6],
 [ 7,  8,  9]])
```

numpy.insert(arr, obj, values, axis=None)其中obj接收整数或者整数序列，表示插入的索引位置。不指定轴向时，将数组都展平后进行追加

特点：有自动补全（循环调用values进行添加）

[[1 2 3]
[4 5 6]]
[[10]
[20]]

print(np.insert(a, 2, b, axis=0)) #向数组a的行方向，索引为2的行插入数组b

[[ 1  2  3]
[ 4  5  6]
[10 10 10]
[20 20 20]]

print(np.insert(a, 1, b, axis=1)) #向数组a的列方向，索引为1的列插入数组b

[[ 1 10 20  2  3]
[ 4 10 20  5  6]]

删改

删除：numpy.delete(arr, obj, axis=None)

obj：接收索引、切片，表示删除这部分数据

array([[1, 2, 3],
     [4, 5, 6]])

np.delete(a, 2, axis=1)  # 轴向为列，删除索引为2的列

array([[1, 2],
     [4, 5]])

修改：使用索引切片获取到该位置的元素后使用=为该位置重新赋值即可

array([[1, 2, 3],
     [4, 5, 6]])\

a[0, 1] = 100

array([[ 1, 100, 3],
     [ 4,  5,  6]]) 

变形

使用reshape改变数组形状

n = np.arange(1,21)
print(n) #[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
print(n.shape) #(20,)

默认状态下n是长度为20的一维数组

n2 = n.reshape((4,5)) #将n变为4行5列的二维数组
print(n2)

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]
 [11 12 13 14 15]
 [16 17 18 19 20]]

n3 = n2.reshape(20) #变成长度为20的一维数组
print(n3) #[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]
n4 = n2.reshape((5,4)) #变成5行4列的二维数组
print(n4) 

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]

若变形后的size不等于原size会报错：

n = n3.reshape(19) #新size较小，报错
n = n3.reshape((5,5)) #新size较大，报错

使用-1表示任意剩余维度长度

n = np.arange(1,21)
n2 = n.reshape(4,-1) #表示第一个维度为4，第二个维度根据size进行自动补齐，最后生成4行5列的数组
n3 = n.reshape(-1,5) #指定5列->4行5列的二维数组
print(n2)

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]
 [11 12 13 14 15]
 [16 17 18 19 20]]

print(n3)

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]
 [11 12 13 14 15]
 [16 17 18 19 20]]

n4 = n2.reshape(-1)
print(n4) #[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20]

注意reshape中只允许出现一个-1

n4 = n2.reshape(3,-1) #报错，20不能被3整除，无法生成3行n列的数组
n4 = n2.reshape(-1,-1) #报错

级联（合并）

np.concatenate((n1,n2),axis=0)将n1和n2合并

axis控制按哪个维度合并，默认为0（第一个维度）；对于二维数组，第一个维度为行，第二个为列

n1 = np.arange(1,21).reshape(4,-1)
n2 = np.arange(21,41).reshape(4,-1)
print(n1)

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]
 [11 12 13 14 15]
 [16 17 18 19 20]]

print(n2)

[[21 22 23 24 25]
 [26 27 28 29 30]
 [31 32 33 34 35]
 [36 37 38 39 40]]

print(np.concatenate((n1,n2))) #默认按行合并（上下合并）

[[ 1  2  3  4  5]
 [ 6  7  8  9 10]
 [11 12 13 14 15]
 [16 17 18 19 20]
 [21 22 23 24 25]
 [26 27 28 29 30]
 [31 32 33 34 35]
 [36 37 38 39 40]]

print(np.concatenate((n1,n2),axis=1)) #按列合并（左右合并）

[[ 1  2  3  4  5 21 22 23 24 25]
 [ 6  7  8  9 10 26 27 28 29 30]
 [11 12 13 14 15 31 32 33 34 35]
 [16 17 18 19 20 36 37 38 39 40]]

注意合并时对应方向的行数/列数要相同（np包不支持用NaN补齐）

np.hstack((n1,n2))水平级联（左右合并），相当于上面的np.concatenate((n1,n2))

np.vstack((n1,n2))垂直级联（上下合并），相当于上面的np.concatenate((n1,n2),axis=1)

分隔

垂直切分：

np.vsplit(n,num)将有m行的数组拆分成num份，每份有m/num行，m/num结果必须是整数，否则报错
np.vsplit(n,(拆分点1,拆分点2,...))在拆分点处将数组切开

[[ 1  2  3  4]
[ 5  6  7  8]
[ 9 10 11 12]
[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]

print(np.vsplit(n,3)) #拆成3份，每份2行

[array([[1, 2, 3, 4],
     [5, 6, 7, 8]]), 
array([[ 9, 10, 11, 12],
     [13, 14, 15, 16]]), 
array([[17, 18, 19, 20],
     [21, 22, 23, 24]])]

print(np.vsplit(n,(1,2,4))) #在第1、2、4行后进行切割

[array([[1, 2, 3, 4]]), 
array([[5, 6, 7, 8]]), 
array([[ 9, 10, 11, 12],
     [13, 14, 15, 16]]), 
array([[17, 18, 19, 20],
     [21, 22, 23, 24]])]

水平切分：np.hsplit(n,num)和np.hsplit(n,(拆分点1,拆分点2,...))用法同上
水平和垂直切分：np.split(n,num,axis=0)和np.split(n,(拆分点1,拆分点2,...),axis=0)，用法同上
- axis控制切分方向，默认为0是按行切分，为1时按列切分

复制

使用=赋值（浅拷贝）：两个ndarray用的是同一个地址，改变一个时另一个也改变
```
n = np.arange(1,6)
n1 = n
n1[0] = 10
print(n,n1) #[10  2  3  4  5] [10  2  3  4  5]
```

深拷贝：n.copy()

n = np.arange(1,6)
n1 = n.copy()
n1[0] = 10
print(n,n1) #[1 2 3 4 5] [10  2  3  4  5]

聚合操作

以求和np.sum(n)为例：

一维数组np.sum(n)

n = np.arange(1,6)
print(n) #[1 2 3 4 5]
print(np.sum(n)) #15

二维数组np.sum(n,axis=None)

默认情况下是求数组中所有数的和
当axis=0时，将每一列的数单独求和
当axis=1时，将每一行的数单独求和

[[ 1  2  3  4  5]
[ 6  7  8  9 10]
[11 12 13 14 15]
[16 17 18 19 20]]

print(np.sum(n)) #所有数的和210
print(np.sum(n,axis=0)) #每一列的多行求和[34 38 42 46 50]
print(np.sum(n,axis=1)) #每一行的多列求和[15 40 65 90]

其它聚合函数：

聚合函数

它们的用法都与sum类似，可以指定维度

一些特殊用法：

n = np.arange(1,11)
print(n) #[ 1  2  3  4  5  6  7  8  9 10]
print(np.percentile(n,q=50)) #百分位数，当q=50时为中位数：5.5
print(np.percentile(n,q=25)) #1/4位数：3.25
n = np.append(n, 10)
print(n) #[ 1  2  3  4  5  6  7  8  9 10 10]
print(np.argmax(n)) #第一个最大值对应的下标：9
print(np.argwhere(n==np.max(n))) #所有最大值的下标[[ 9],[10]]
print(np.power(n,2)) #将所有数都平方[  1   4   9  16  25  36  49  64  81 100 100]

排除nan空值（是float类型）：使用np.nanxxx(n)系列函数

n = np.array([1,2,3,np.nan])
print(np.sum(n)) #nan
print(np.nansum(n)) #6.0

同理上面的聚合函数都有nan版本，如nanmax、nanmin等等

矩阵操作

基本操作

加减乘除

n + 10就是将n中每个元素都+10，- * / //（整除） **次方 %取模同理

[[1 2 3]
 [4 5 6]]

print(a*2)

[[ 2  4  6]
 [ 8 10 12]]

a + b就是将两个矩阵的对应元素相加，其它符号同理

[[1 2 3]
 [4 5 6]]
[[2 3 4]
 [5 6 7]]

print(a+b)

[[ 3  5  7]
 [ 9 11 13]]

线性代数

两矩阵相乘：np.dot(n1,n2)其中n1的列数必须等于n2的行数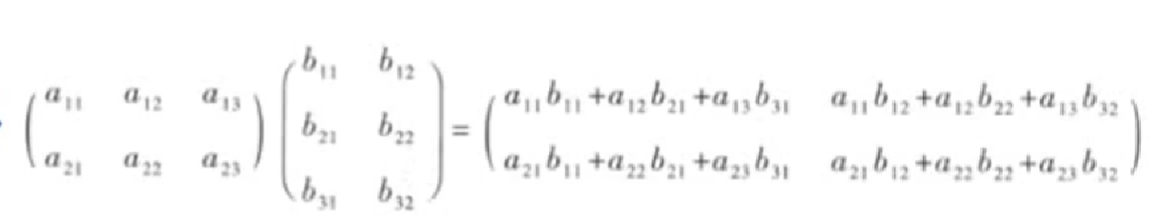

矩阵相乘

[[1 2 3]
[4 5 6]]
[[ 1  2  3  4]
[ 5  6  7  8]
[ 9 10 11 12]]

print(np.dot(a,b))

[[ 38  44  50  56]
[ 83  98 113 128]]

逆矩阵：np.linalg.inv(a)
行列式：np.linalg.det(a)，如有计算误差，使用np.round(res)消除最后多余的小数
矩阵的秩：np.linalg.matrix_rank(a)

广播机制

当矩阵运算出现维度缺失或元素缺失时：

为缺失的维度补维度
缺失元素用已有值填充

例1：

[1 2 3]  # a为(1,3)
[[1 2 3] 
 [4 5 6]]  # b为(2,3)

求a+b：加法要求对应元素相加，a缺少一行（缺维度），此时就要补上一行，这行的值来自已有元素，即将第一行的值复制到第二行

print(a+b)

[[2 4 6]
 [5 7 9]]

例2：

[[1]
 [2]
 [3]]
[1 2 3]

print(a+b)  # 将a的第一列复制到第二、三列，将b的第一行复制到第二、三行

[[2 3 4]
 [3 4 5]
 [4 5 6]]

其它常见数学操作

绝对值：np.abs(n)
平方根：np.sqrt(n) 等同于 n**0.5
平方：np.square(n) 等同于 n**2
以e为底的指数：np.exp(n)（e的n次方）
自然对数(ln)：np.log(n) np.log(np.e)即ln(e)=1
以2/10为底的对数：np.log2(n)/np.log10(n)
三角函数：np.sin(n)/np.cos(n)/np.tan(n)等
四舍五入：np.round(n, m)保留m位小数
取整：
- 向上取整：np.ceil(n)（1.1->2）
- 向下取整：np.floor(n)（1.1->1）

累加：np.cumsum(n)将n中第m个元素设置为前m个元素的和

# [1 2 3 4 5 6 7 8 9]
print(np.cumsum(b))  # [ 1  3  6 10 15 21 28 36 45]

排序

np.sort(a, axis=-1, kind='quicksort', order=None)不改变原数组，返回排序后数组

axis：要排序的维度
kind：排序方法（一般默认）
order：指定排序的规则

a = np.random.randint(0,10,size=6)
print(a) #[5 2 0 3 1 5]
print(np.sort(a)) #升序 [0 1 2 3 5 5]
print(np.sort(a)[::-1]) #降序 [5 5 3 2 1 0]
print(a) #[5 2 0 3 1 5]不改变原数组

ndarray.sort()直接改变原数组，不返回

a = np.random.randint(0,10,size=6)
print(a) #[7 0 5 9 0 4]
print(a.sort()) #None 因为无返回值
print(a) #升序[0 0 4 5 7 9]
a = a[::-1]
print(a) #降序[9 7 5 4 0 0]

文件操作

保存/读取数组

np.save(路径,ndarray)：将一个数组保存到npy文件中
np.savez(路径,数组名1=数组1,数组名2=数组2,...)：将多个数组保存到npz文件中

x=np.arange(5)
y=np.arange(10,20)
np.save('test_data/x',x)
np.savez('test_data/xy',xarr=x,yarr=y)

np.load('路径')读取npy/npz，其中读取npy文件时直接返回其中保存的数组，npz文件需要用键（数组名）来取值（对应的数组）

X=np.load('test_data/x.npy')
XY_x=np.load('test_data/xy.npz')['xarr']
XY_y=np.load('test_data/xy.npz')['yarr']
print(X,XY_x,XY_y)

[0 1 2 3 4] [0 1 2 3 4] [10 11 12 13 14 15 16 17 18 19]

读写csv/txt文件

np.savetxt(txt/csv路径,ndarray,delimeter='\n')delimeter为分隔符，txt和csv文件都用savetxt函数

x=np.arange(5)
np.savetxt('test_data/newx.csv',x)

np.loadtxt(txt/csv路径,delimeter='\n')delimeter为分隔符

X=np.loadtxt('test_data/newx.csv',dtype=np.int16)
print(X) #[0 1 2 3 4]

练习题

创建一个长度为10的一维全为0的nd对象，让第5个元素=1

n1 = np.zeros(10,dtype=np.int16)
n1[4] = 1
print(n1)  # [0 0 0 0 1 0 0 0 0 0]

创建一个元素从10到19的nd对象

n2 = np.arange(10, 20)
print(n2)  # [10 11 12 13 14 15 16 17 18 19]

反转上面的数组

print(n2[::-1])  # [19 18 17 16 15 14 13 12 11 10]

使用random创建一个5*5的nd对象，输出最值

n4 = np.random.random(size=(5,5))
print(n4, np.max(n4), np.min(n4))

[[0.66469851 0.61117541 0.32542287 0.09506143 0.16963662]
[0.28704474 0.76092083 0.61811267 0.44801328 0.30261958]
[0.00131316 0.46701248 0.23806467 0.41173001 0.82038262]
[0.9854772  0.79781505 0.52325213 0.41652154 0.66836552]
[0.67058969 0.83924063 0.43948989 0.61249562 0.65736923]] 
0.9854772008163543 0.0013131649777491372

创建一个5*5的nd对象，边界为1，里面为0

n5 = np.zeros((5, 5), dtype=np.int16)
n5[[0, -1]] = 1  # 让第一行和最后一行为1
n5[:, [0, -1]] = 1  # 让第一列和最后一列为1

# 第二种方式，全为1，再让第1-4行第1-4列为0
n5 = np.ones((5, 5), dtype=np.int16)
n5[1:-1, 1:-1] = 0
print(n5)

[[1 1 1 1 1]
[1 0 0 0 1]
[1 0 0 0 1]
[1 0 0 0 1]
[1 1 1 1 1]]

创建一个每行都是0-4的5*5矩阵

l = [0, 1, 2, 3, 4] * 5  # [0,1,2,3,4]重复5次
n6 = np.array(l).reshape((5, 5))
print(n6)

[[0 1 2 3 4]
[0 1 2 3 4]
[0 1 2 3 4]
[0 1 2 3 4]
[0 1 2 3 4]]

创建一个[0,1]间长度为5的等差数列

n7 = np.linspace(0, 1, 5)
print(n7)  # [0.   0.25 0.5  0.75 1.  ]

创建一个长度为10的随机数组并排序

n8 = np.random.randint(-5, 5, 10)
print(n8.sort())  # [-5 -3 -2 -1  1  1  1  2  2  3]

创建一个长度为10的随机数组并将最大值替换为0

n9 = np.random.randint(-5, 5, 10)
print(n9)
max_value = np.max(n9)
for i in range(len(n9)):
    if n9[i] == max_value:
        n9[i] = 0
print(n9)

# 也可直接使用argwhere函数
n9 = np.random.randint(-5, 5, 10)
print(n9)  # [ 4 -2  2 -4  2 -5  3  2  0 -4]
max_index = np.argwhere(n9 == max_value)
print(max_index)
# [[5]
#  [7]] 需要转成一维形式
max_index = max_index.reshape(-1)  # 不确定长度，只知道要转成一维，使用reshape(-1)
print(max_index)  # [5 7]
n9[max_index] = 0  # 可以使用nd数组作索引集合，不非得是列表
print(n9)

给定一4维矩阵，求最后两维的和

n10 = np.random.randint(1, 10, size=(2, 3, 4, 5))
print(n10.sum(axis=(2,3)))  # 第一个维度是axis=0，第三四个维度就是23

[[106 106 110]
[106 100  90]]

给定数组[1,2,3,4,5]，在每个元素间插入3个0

n = np.array([1, 2, 3, 4, 5])
n11 = np.zeros(4*3+5, dtype=np.int16)  # 共含17个0的数组，每隔3个数就添加给定数组中的一个数
n11[::4] = n  # n11[::4]就是步长为5进行取数即n11[[0,4,8,12,16]] = n[[0,1,2,3,4]]
print(n11)  # [1 0 0 0 2 0 0 0 3 0 0 0 4 0 0 0 5]

给定二维矩阵，交换其中两行元素

n12 = np.arange(0, 10).reshape((2, -1))
print(n12)

[[0 1 2 3 4]
[5 6 7 8 9]]

n12 = n12[[1, 0]]
print(n12)

[[5 6 7 8 9]
[0 1 2 3 4]]

不同方法求数组的三次方，比较运行时间

n = np.random.randint(0, 10, size=100000)
import timeit
start = timeit.default_timer()
np.power(n, 3)
end = timeit.default_timer()
print(end-start)  # 0.0002852
start = timeit.default_timer()
n**3
end = timeit.default_timer()
print(end-start)  # 0.0001768

创建一个5*3的矩阵和一个3*2的矩阵，求矩阵积

n1 = np.arange(1, 16).reshape((5, -1))
n2 = np.arange(1, 7).reshape((3, -1))
print(np.dot(n1, n2))

[[ 22  28]
[ 49  64]
[ 76 100]
[103 136]
[130 172]]

矩阵每一行元素都减去该行的平均值

n = np.arange(1, 16).reshape((5, 3))
mean = n.mean(axis=1).reshape(5, 1)  # 变成5行1列的才能与5行3列的相减
print(n - mean)

[[-1.  0.  1.]
[-1.  0.  1.]
[-1.  0.  1.]
[-1.  0.  1.]
[-1.  0.  1.]]

创建一个5*5的zero矩阵，变成下面的矩阵

[[0 1 0 1 0]
[1 0 1 0 1]
[0 1 0 1 0]
[1 0 1 0 1]
[0 1 0 1 0]]

n = np.zeros((5, 5), dtype=np.int16)
# 可以看到奇数行中的第偶数个元素变为1
n[::2, 1::2] = 1  # ::2取奇数行，1::2取偶数个
# 可以看到偶数行中的第奇数个元素变为1
n[1::2, ::2] = 1  # 1::2取偶数行，::2取奇数个

正则化（归一化）一个5*5随机矩阵

正则化：每个元素a=(a-min)/(max-min)，其中max/min为矩阵元素最值

n = np.random.randint(0, 100, size=(5, 5))
min = n.min()
max = n.max()
n = (n-min)/(max-min)
print(np.round(n,3))  # 结果中每个元素都在0-1范围内

[[0.701 0.691 1.    0.711 0.402]
[0.031 0.495 0.124 0.515 0.753]
[0.639 0.567 0.928 0.773 0.062]
[0.052 0.835 0.732 0.    0.629]
[0.588 0.557 0.103 0.206 0.557]]