加载页面中...
principle | lwstkhyl

principle

other-other

文章涉及到的一些基本概念，算法/分析的原理

来自nature文章Improved prediction of immune checkpoint blockade efficacy across multiple cancer types

具体代码实现详见我的GitHub仓库

数据说明

一些概念

免疫检查点(Immune Checkpoint)：细胞中程序性死亡受体及其配体

ICB(immune checkpoint blockade)：免疫检查点阻断，指通过抑制程序性死亡受体及其配体的结合，从而提高宿主免疫系统对肿瘤细胞的攻击性

TMB：肿瘤突变负荷，指每百万碱基检测出的体细胞变异总数。在多数肿瘤细胞中，TMB越高，产生的新抗原越多，肿瘤免疫原性越高，越容易被免疫细胞识别，从PD-1/PD-L1免疫检查点抑制剂治疗中的获益越显著

MSI：微卫星不稳定性，指肿瘤中某个微卫星位点由于重复单元的插入或缺失而出现新的微卫星等位基因的现象。也常用于预测肿瘤预后，绝大多数MSI不稳定性高的患者，TMB都高；但TMB高的，MSI不稳定性不一定高

CNV/CNA：拷贝数变异，由基因组发生重排而导致，一般指长度1KB以上的基因组大片段的拷贝数增加或者减少，是基因组结构变异的重要组成部分

LOH：杂合性缺失，位于一对同源染色体上的相同基因座位的两个等位基因中的一个（或其中部分核苷酸片段）发生缺失，与之配对的染色体上仍然存在，最后一对等位基因只剩下其中一个，可能导致该基因的失活

生存相关：

  • 总生存时间OS：从记录开始至（因任何原因）死亡的时间

  • 无进展生存期PFS：从记录开始到肿瘤发生（任何方面）进展或（因任何原因）死亡的时间。增加了“发生恶化”这一节点，而“发生恶化”往往早于死亡，所以PFS常常短于OS，因而随访时间短一些。PFS的改善包括了“未恶化”和“未死亡”，即间接和直接地反映了临床获益，它取决于新治疗与现治疗的疗效/风险

逻辑回归模型(logistic regression model)：根据给定的自变量数据集来估计事件的发生概率，要求因变量是一个二分类变量（即只能取两个值的变量，比如这篇论文中就是“对ICB治疗有/无反应”），结果是事件发生的概率，这篇论文中就是“对ICB治疗有反应的概率”

样本统计指标总结：

  • 真阳性(TP)：模型正确地将正样本预测为正类

  • 真阴性(TN)：模型正确地将负样本预测为负类

  • 假阳性(FP)：模型错误地将负样本预测为正类

  • 假阴性(FN)：模型错误地将正样本预测为负类

  • 灵敏度(Sensitivity)/召回率(Recall)/真正率(TPR)：在所有实际为正类的样本中，被预测为正类的比例–TP/(TP+FN)

  • 特异性(Specificity)：在所有实际为负类的样本中，被预测为负类的比例–TN/(TN+FP)

  • 准确率(Accuracy)：所有样本中被正确分类的比例–(TP+TN)/(TP+TN+FP+FN)

  • 精确率(Precision)/阳性预测值(PPV)：在所有被预测为正类的样本中，实际为正类的比例–TP/(TP+FP)

  • 阴性预测值(NPV)：在所有被预测为负类的样本中，实际为负类的比例–TN/(TN+FN)

  • 假正率(FPR)：在所有实际为负类的样本中，被预测为正类的比例–1-特异性=FP/(FP+TN)

ROC曲线：横轴为FPR（假正率），指所有负类样本中，被错误预测为正类的比例；纵轴为TPR（真正率），指所有正类样本中，被正确预测为正类的比例。理想情况下，TPR=1，FPR=0，即图的(0,1)点，所以ROC曲线越靠左上角，预测效果越好

  • AUC(Area Under Curve)；ROC曲线下的面积，值越大则预测效果越好

    • AUC值接近1：模型预测准确率高

    • AUC值略大于0.5：模型预测准确率一般

    • AUC值等于0.5：相当于没有预测效果

    • AUC值小于0.5：相当于反向预测，一般情况下不会出现

  • 最优阈值(optimal threshold)：前面说过，对于二分类模型，模型对于每个样本会给出一个概率值。现需要寻找一个阈值，当概率值超过这个阈值时，说明模型将该样本预测为正类，反之为负类。当预测效果最好（TPR和FPR差值最大）时，这个阈值就称为最优阈值 具体实现过程

PRC曲线：先看平滑不平滑（越平滑越好），再看谁上谁下（同一测试集、一般情况下，上面的比下面的好）

更多关于这两种曲线

两种曲线

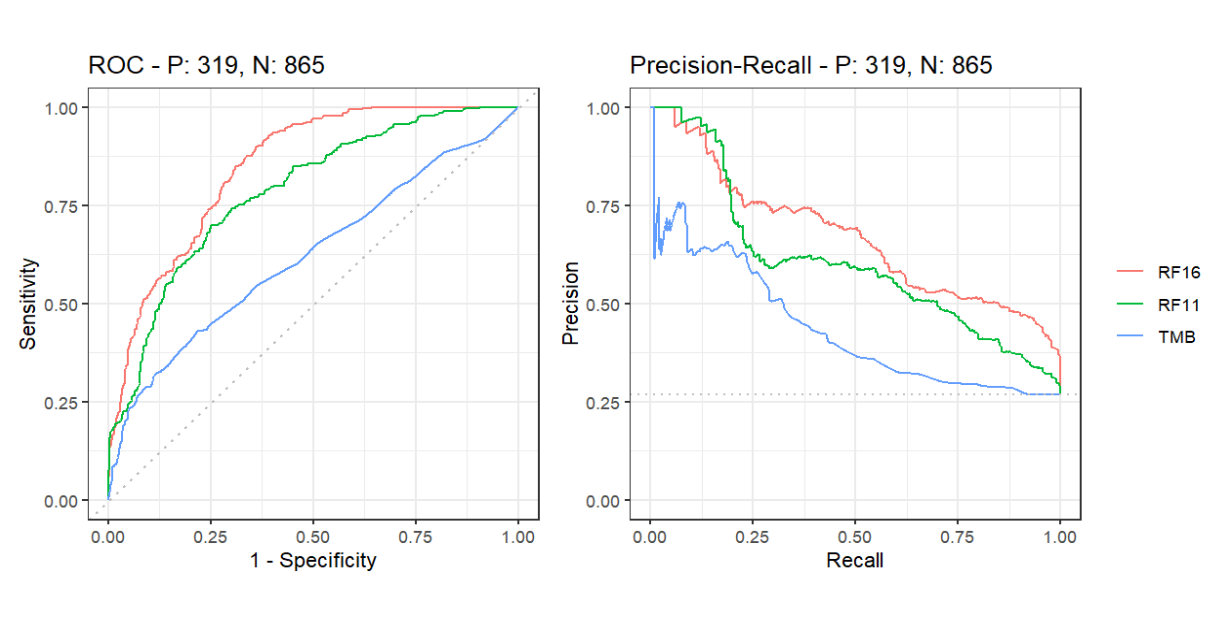
如图，红线>绿线>蓝线

泛癌(pan-cancer)分析：针对某一个特征横向比较多个癌型，看其敏感性和特异性。其实就是把所有种类（或者说多个种类）的癌症都纳入分析范围

Brier score：预测概率与实际结果之间的均方差，取值为0-1，值越小模型预测效果越好

一致性指数C-index：类似于AUC，也是用来评价模型的预测能力。通常取值0.5-1，值越大预测效果越好

  • 0.5-0.7：较低准确度

  • 0.71-0.9：中等准确度

  • >0.9：高准确度

计算方法：把所有研究对象随机每2个划为一组。例如在生存分析中，对于一组患者，如果生存时间较长的那个人的预测生存时间也较长，则称之为预测结果与实际结果一致

风险比(HR)：用于评估一个二分类因素对生存状态的影响。越远离1，影响越大。比如评估“性别”对患者死亡概率的影响，计算女性对男性的风险比

  • HR=1：男性女性死亡速度相同，性别无影响

  • HR>1：女性风险更高，值越大，风险越大。例如HR=2，就是女性死亡速度是男性的2倍

  • HR<1：女性风险更低，值越小，风险越小。例如HR=0.5，就是女性死亡速度是男性的一半

95%置信区间(CI)：用同样的步骤，去计算置信区间，那么如果重复独立地计算100次，有95%的概率计算出来的区间会包含真实参数值，即大概会有95个置信区间会包含真值。虽然它不是指“CI有95%的概率包括真实参数”，但可以认为真实参数大概率就在CI内，因此通常把CI作为目标参数可能取值的上下界

混淆矩阵：展示模型对各类样本的预测情况。混淆矩阵的第i行第j列为实际为i类的样本被预测为j类的比例。例如

混淆矩阵

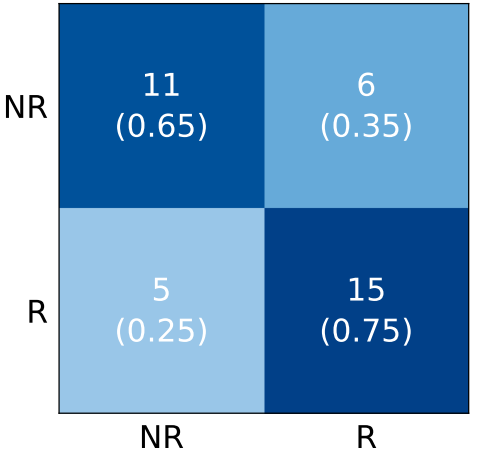
已知横坐标是预测值，纵坐标是实际值，左下角的块就表示预测是NR但实际为R的样本数量和比例。可以看出，(NR, NR)和(R, R)这两个块的值应越大越好->如果值越大颜色越深，那么就是左上-右下对角线上的块颜色越深，模型预测效果越好

源数据各列含义

列名 含义 补充
SAMPLE_ID 样本编号  
Cancer_type_grouped_2
Cancer_Type2
Cancer_Type		 癌症类型  
Chemo_before_IO 患者在免疫治疗前是否接受化疗 1接受
0没接受
Age 年龄  
Sex 性别 1男性
0女性
BMI 体重指数  
Stage 肿瘤分期 1表示IV期
0表示I-III期
Stage at IO start 患者在免疫治疗前的肿瘤分期  
NLR 血液中性粒细胞与淋巴细胞比值  
Platelets 血小板水平  
HGB 血红蛋白水平  
Albumin 白蛋白水平  
Drug 使用的免疫治疗药物 0使用PD1/PDL1或CTLA4
1同时使用这两种
Drug_class 使用的免疫治疗药物名称  
TMB 肿瘤突变负荷  
FCNA 拷贝数改变分数  
HED HLA-I的进化差异  
HLA_LOH HLA-I杂合性缺失状态  
MSI 微卫星不稳定性 1不稳定
0稳定/不确定
MSI_SCORE 微卫星不稳定性得分  
Response 是否有应答 1应答者
0非应答者
OS_Event 是否死亡 1死亡
0存活
OS_Months 总生存时间 以月为单位
PFS_Event 是否死亡/肿瘤是否发生恶化 1发生
0没发生
PFS_Months 无进展生存期 以月为单位
RF16_prob
RF11_prob		 不属于源数据，是通过sklearn得到的值  

Response补充说明：将接受了PD-1/PD-L1抑制剂、CTLA-4阻断剂或两种免疫疗法的联合治疗的患者分为不同组

  • 出现完全应答complete response(CR)或部分应答partial response(PR)的患者——应答者responders(R)

  • 疾病无变化stable disease(SD)或发生进展progressive disease(PD)的患者——非应答者non-responders(NR)

算法分析

在方法一栏中，其中Patient data description、Response, OS and PFS、Genomic, demographic, molecular and clinical data都是在说源数据是怎么来的，以及数据的划分、处理方法、具体含义等等，主要核心的大概是下面几部分

Model description

作者采用了随机森林分类器的方法来训练出相关模型，同时对随机森林的超参数预设也做出的相应的测试优化，即使用网格搜索(GridSearchCV)来找到随机森林分类器的最佳超参数，并评估这些与免疫疗法疗效相关的生物学特征对预测模型的贡献

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习(Ensemble Learning)方法

从直观角度来解释，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的Bagging思想

打个形象的比喻：森林中召开会议，讨论某个动物到底是老鼠还是松鼠，每棵树都要独立地发表自己对这个问题的看法，也就是每棵树都要投票。该动物到底是老鼠还是松鼠，要依据投票情况来确定，获得票数最多的类别就是森林的分类结果。森林中的每棵树都是独立的，99.9%不相关的树做出的预测结果涵盖所有的情况，这些预测结果将会彼此抵消。少数优秀的树的预测结果将会超脱于芸芸“噪音”，做出一个好的预测。将若干个弱分类器的分类结果进行投票选择，从而组成一个强分类器

随机森林还有一个特点是“随机性”，具体来说，有以下两种：

  • 样本随机性：在训练每棵决策树时，随机森林会从原始训练集中抽取一个样本子集（通常使用有放回抽样）。

  • 特征随机性：在每个决策节点，随机森林不是考虑所有特征，而是随机选择一部分特征，然后从中选择最佳分裂特征。

随机森林的构建过程：

  • 构建决策树：对于随机森林中的每棵树，都进行以下步骤
    • 从训练集中随机抽取样本（有放回）。
    • 在每个节点，随机选择一部分特征，并基于这些特征选择最佳分裂点。
    • 递归地分裂节点，直到满足停止条件（如节点中的样本数小于某个阈值，或达到树的最大深度）。
  • 森林中树的生成规则为：
    • 如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本（bootstrap sample采样），作为该树的训练集；
    • 如果每个样本的特征维度为M，指定一个常数m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这m个特征中选择最优的；
    • 每棵树都尽最大程度的生长，并且没有剪枝过程。
  • 聚合预测：对于分类问题，随机森林通过多数投票的方式来进行预测。即每棵树给出一个类别预测，最终选择得票最多的类别作为最终预测结果。

一些问题：

  • 每棵树的训练集都是不同的，而且里面包含重复的训练样本。
  • 为什么要随机抽样训练集：如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的，这样的话完全没有bagging的必要；
  • 为什么要有放回地抽样：如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是”有偏的”，都是绝对”片面的”，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决，这种表决应该是”求同”，所以说使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的

Logistic regression analysis

逻辑回归模型：根据给定的自变量数据集来估计事件的发生概率，要求因变量是一个二分类变量（即只能取两个值的变量，比如这篇论文中就是“对ICB治疗有/无反应”），结果是事件发生的概率（这篇论文中就是“对ICB治疗有反应的概率”）。它使用最大似然估计来估计模型参数。给定数据集，我们寻找参数值，使得观察到的数据出现的概率最大

逻辑函数（也称为sigmoid函数）定义为：

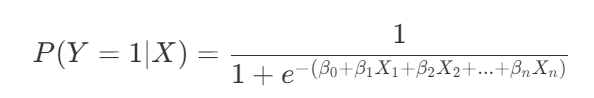
Logistic3

其中，β0,β1,…,βn是模型参数，X1,X2,…,Xn是预测变量

Logistic模型的创建过程可以使用R中的glm函数，并使用MASS包中的stepAIC函数进行模型选择，以下是一个简单的例子（因为作者这里没有给出源代码，只能模拟一下）：

  • 模型拟合：使用glm(formula, data, family)（广义线性模型）来拟合逻辑斯蒂回归模型
    • formula：数据关系，如y~x1+x2+x3
    • family：数据分布
    # 拟合逻辑斯蒂回归模型
model <- glm(formula, family=family.generator, data,control = list(…))

  • 模型选择：使用MASS包中的stepAIC函数进行模型选择，它通过逐步回归和赤池信息准则（AIC）来选择模型

    # 加载MASS包
library(MASS)
# 模型选择
selected_model <- stepAIC(model, direction = "both")

  • 模型预测：使用predict函数来获取测试集中样本的响应概率

    # 预测测试集结果
predictions <- predict(selected_model, newdata = test_data, type = "response")

  • 计算标准化系数：使用reghelper包中的beta函数来计算标准化系数，这有助于比较不同变量的影响大小

    # 加载reghelper包
library(reghelper)
# 计算标准化系数
standardized_coefficients <- beta(selected_model)
  • 最后就可以进行模型评估（例如混淆矩阵、ROC曲线、AUC值等），计算模型的性能

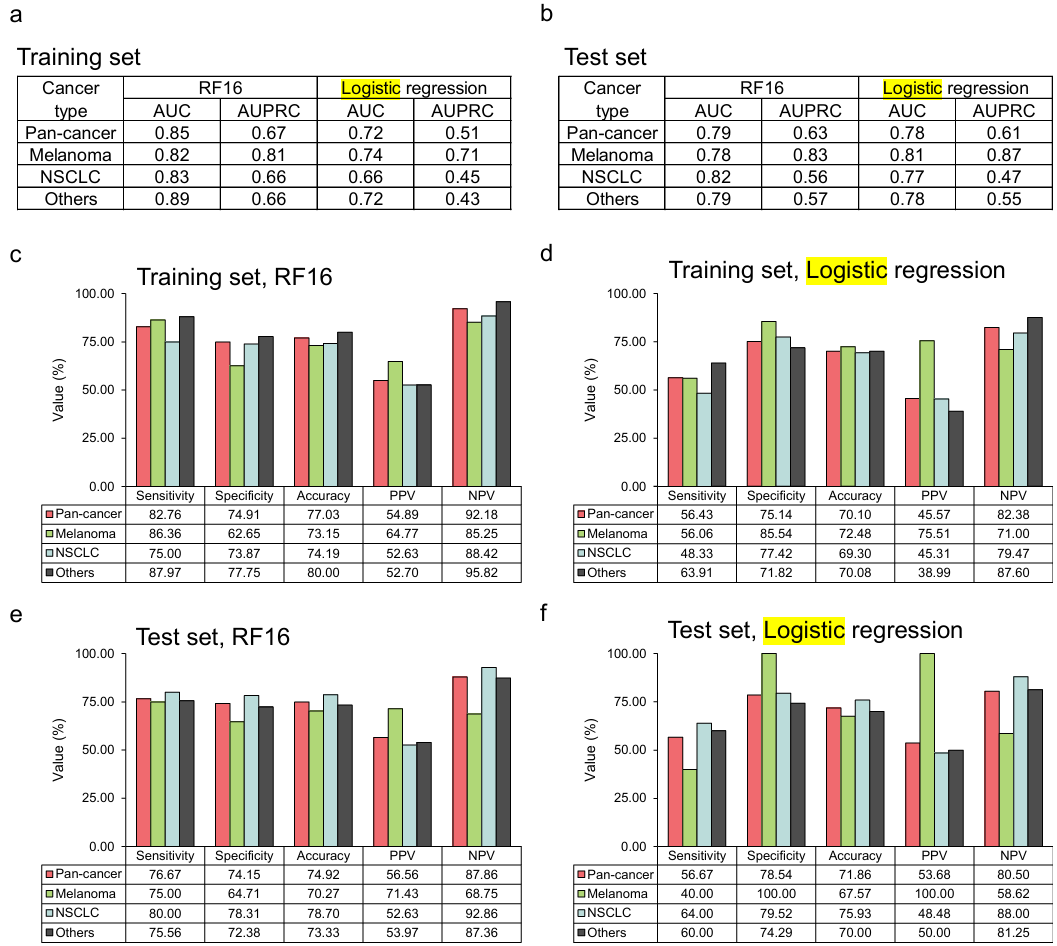
这篇文章中，作者将RF16模型与使用相同训练数据和模型特征的logistic回归模型进行比较。计算了由逻辑回归估计的模型特征及其相应的P值

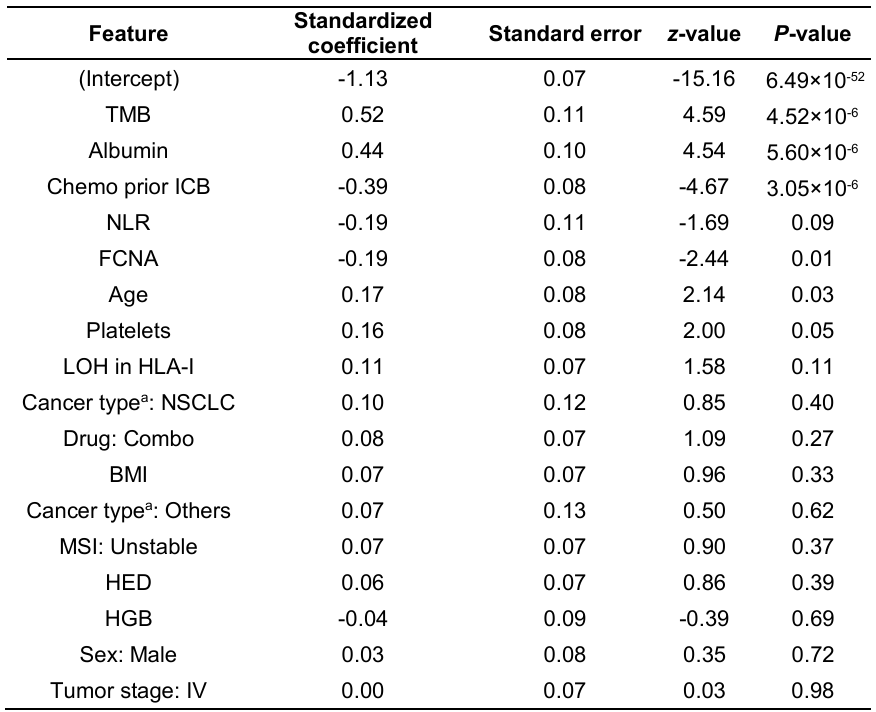
Logistic1

结果表明：与泛癌、黑色素瘤、NSCLC和其他癌症的logistic回归相比，RF16模型在训练集和测试集中始终实现了更高的预测性能

Logistic2

ROC and precision-recall curve analyses

ROC曲线：常用于二分类问题中的模型比较，主要表现为一种真阳性率(TPR)和假假阳性率(FPR)的权衡，用于确定分类器在某一阈值下对二分类问题的预测准确性

roc2

以TPR为纵轴，FPR为横轴，作图，可得到ROC曲线

roc1

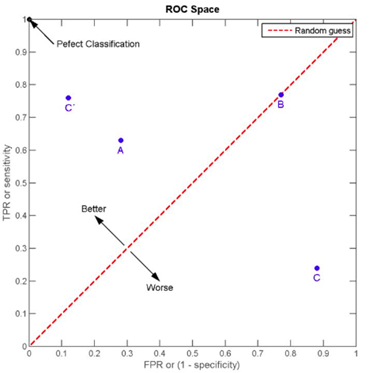
[0, 0]到[1, 1]的虚线即为随机线，该线上所有的点都表示该阈值下TPR=FPR，意味着无论一个样本本身是阴性还是阳性，分类器预测其为正例的概率是一样的，这等同于随机猜测

AUC(Area Under Curve)；ROC曲线下的面积。从图中可以看到位于随机线上方的点（如图中的A点）被认为好于随机猜测。在这样的点上TPR总是大于FPR，意为正例被判为正例的概率大于负例被判为正例的概率，因此AUC越接近1，说明分类器的准确性越高

ROC曲线的绘制方法：对于有有P个阳性，N个阴性的样本集合，首先拿到分类器对于每个样本预测为正例的概率，根据概率对所有样本进行逆序排列，然后将分类阈值设为最大，即把所有样本均预测为反例，此时图上的点为(0,0)，然后将分类阈值依次设为每个样本的预测概率，即依次将每个样本划分为阳性，如果该样本为真阳性，则TP+1; 如果该样本为阴性，则FP+1。最后的到所有样本点的TPR和FPR值，用线段相连

最优阈值(optimal threshold)：对于二分类模型，模型对于每个样本会给出一个概率值。现需要寻找一个阈值，当概率值超过这个阈值时，说明模型将该样本预测为正类，反之为负类。当预测效果最好（TPR和FPR差值最大）时，这个阈值就称为最优阈值

在这篇文章中，作者使用了Youden指数法确定最佳阈值，它是一种常用于选择最佳分类阈值的统计度量，其值为TPR-FPR。对于每个阈值，计算出Youden指数，找到Youden指数最大的那个阈值，这个阈值被认为是最优的分类阈值，这个阈值对应的模型性能在平衡了敏感性和特异性的情况下达到了最佳

PRC曲线：精确率(Precision)-真阳性率(TPR)的曲线，PRC与ROC的相同点是都采用了TPR (Recall)参数，都可以用AUC来衡量分类器的效果。不同点是ROC曲线使用了FPR，而PR曲线使用了精确率

roc3

一般而言，对于同一数据集，PRC曲线越平滑、越靠上，模型预测性能越好

PR曲线的两个指标都聚焦于阳性，因此，在主要关心阳性的类别不平衡问题（某一样例总数远大于另一样例的问题）中，PR曲线被广泛认为优于ROC曲线。例如有998个反例，但是正例只有2个，那么学习方法只需要返回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度；然而这样的学习器往往没有价值，因为它不能预测出任何正例。类别不平衡问题中ROC曲线会作出一个比较乐观的估计，而PR曲线则因为Precision的存在，会受到FP的影响，导致AUC低于ROC曲线

在这篇文章中，作者绘制了测试组和训练组的ROC和PRC曲线，结果均显示RF16模型的预测能力最高

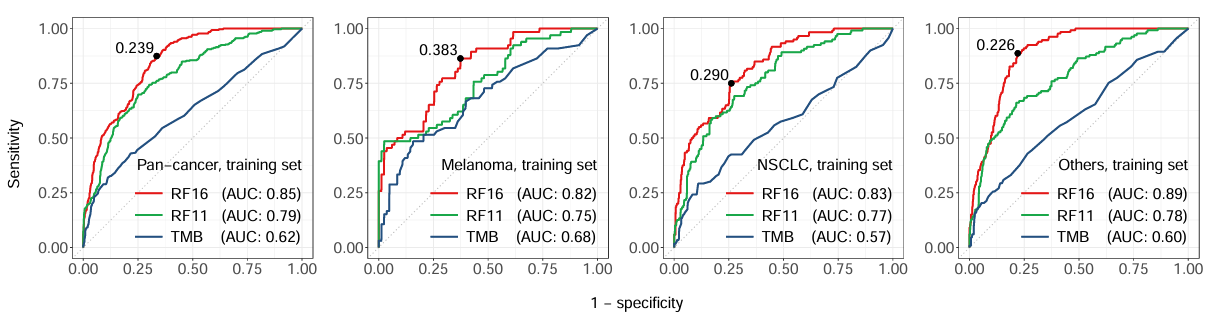
ROC曲线2

两种曲线

Statistical analyses

为了比较RF16模型和TMB在组之间响应概率分布，作者使用了双侧Mann-Whitney U检验，这是一种非参数统计检验，适用于数据不具有正态分布的情况，可以评估两个抽样群体是否可能来自同一群体，进而判断模型的预测性能是否有显著差异。作者还使用了Spearman秩检验计算泛癌和癌症特异性模型响应概率之间的相关系数，以评估两类模型间的差异

之后作者通过计算了RF16模型和TMB的C-index，并使用配对学生t检验对结果进行了比较。一致性指数C-index类似于AUC，也是用来评价模型的预测能力，它把所有研究对象随机每2个划为一组。例如在生存分析中，对于一组患者，如果生存时间较长的那个人的预测生存时间也较长，则称之为预测结果与实际结果一致。通常取值0.5-1，值越大预测效果越好（0.5-0.7为较低准确度，0.71-0.9为中等准确度，高于0.9为高准确度）

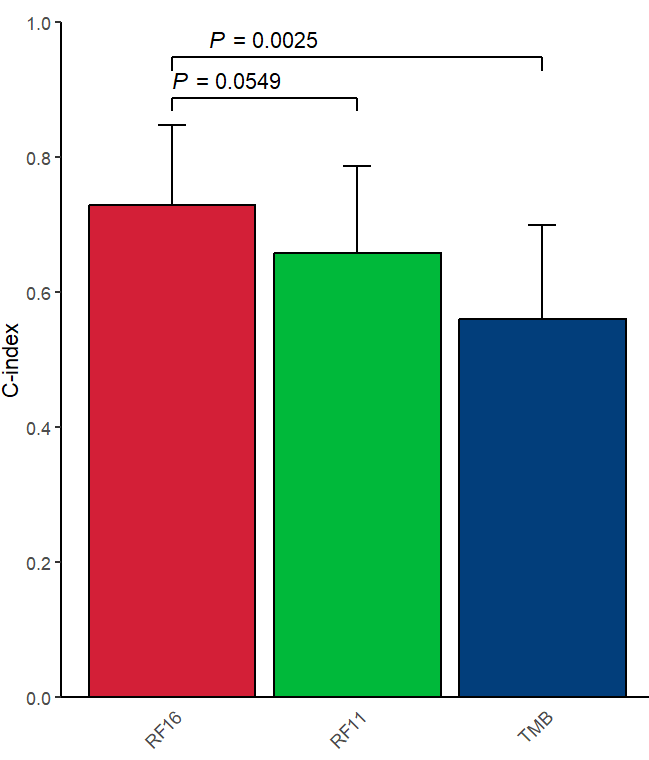
cindex2

图中upper_cindex是误差，这里作为误差棒的上界。可以看到RF16的cindex值较高，且与另两组间p值基本都<0.05，说明RF16显著优于另两组模型

作者还计算了Brier评分，用于衡量模型预测的死亡可能性和实际患者的结局之间的差异，取值为0-1，值越小模型预测效果越好。通常情况下，Brier评分高于0.25表明模型的预测不太准确，小于0.1则模型预测性能优秀

对于二分类问题：

Brier_score

可视化：

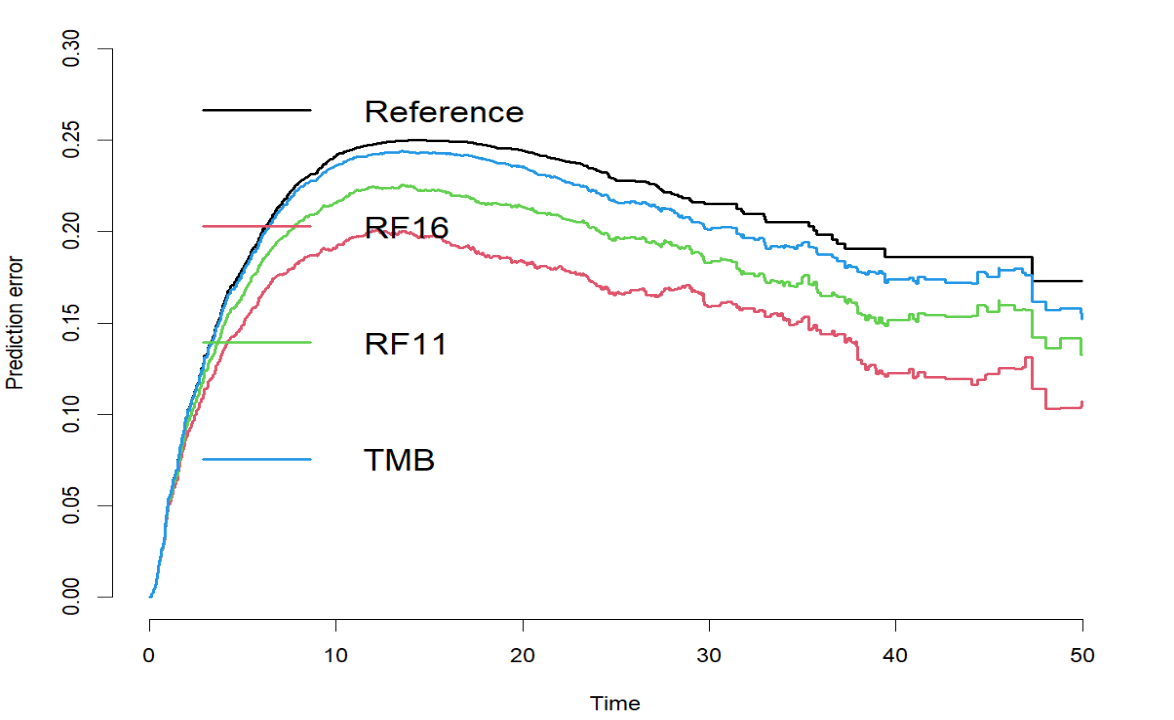
Brier_score2

该图(Prediction error curves)展示了模型对不同生存时间的患者的预测能力，纵坐标是Brier score，因此曲线越靠下预测效果越好。可以看到RF16（红色线）对生存状态的预测能力几乎也是最好的

最后作者进行了KM生存分析和Cox分析。Cox回归主要探讨终点事件发生速度有关的因素，通俗来说，它可以探讨，到底哪类群体的“死亡”速度更快、到底什么因素影响了“死亡”速度。

生存分析的“死亡”指的是，阳性终点事件的发生；死亡速度指的是，t时刻存活的个体在t时刻的瞬时死亡（阳性事件发生）率，可以理解为一组人群在不同时刻的阳性终点事件发生的速度，我们称其为风险h(t)

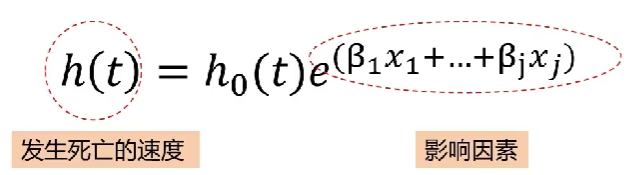单因素cox分析其中h0(t)为常数

在该案例中作者根据RF16模型的预测结果，将样本分为R（有应答）和NR（无应答）两组，探究R与NR与疾病进展速度的关系，即R相对于NR，“死亡”速度的升高了还是降低了？升高了多少倍？降低了多少比例？可用式子hR(t)/hNR(t)计算，最终化简为eβ，即HR（风险比）。HR值大于1，说明暴露因素（R/NR）是阳性事件（死亡）发生的促进因素；小于1，是阻碍因素；等于1，说明无影响

以测试组–Melanoma–OS为例：

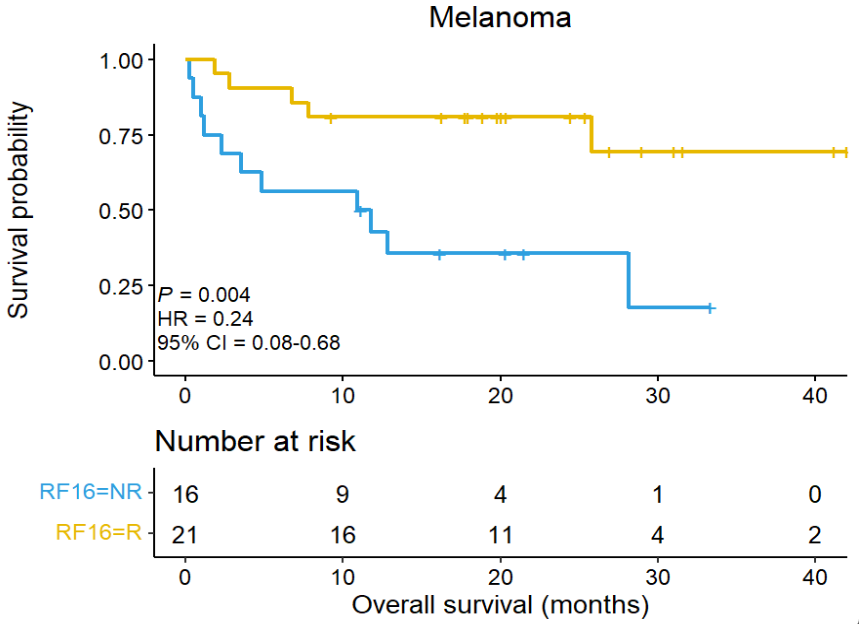
Survival1

横坐标是时间，下面图的纵坐标是存活人数，即在两组中，在对应时间有多少人还存活；上面图的纵坐标是生存概率，根据下面图的存活人数/总人数计算得到

可以看到R组的生存概率明显高于NR组，HR值为0.24（远小于1），p值<0.05且CI没有跨过“1”这个点（这说明得到的HR有统计学意义），说明相比NR个体，R个体总体死亡速度减缓了24%，模型的分组能较准确地预测生存状态